Préambule : Un petit historique
Avant de pouvoir comprendre comment fonctionne Ethereum, il est nécessaire de comprendre la technologie blockchain de manière générale. Pour éviter toute confusion, il est bon de savoir qu’il n’y a pas une seule et unique blockchain. Le terme blockchain désigne un concept abstrait qui peut être implémenté de multiples manières. Le concept a été défini pour la première fois par Satoshi Nakamoto en 2008 et déployé pour supporter la plateforme Bitcoin en 2009. Bien que la blockchain Ethereum soit différente de la blockchain Bitcoin sur bien des points, ces deux plateformes partagent les mêmes principes fondamentaux. Avant de s’attaquer à Ethereum, il va donc falloir passer par Bitcoin.
Bitcoin est un système de paiement digital s’appuyant sur une crypto-monnaie du même nom. Comme dans tout système de paiement dématérialisé, il est nécéssaire de maintenir un registre des comptes pour connaitre la balance de chaque utilisateur. Dans le monde « réel », ce sont les banques qui tiennent ce registre. Si l’on souhaite envoyer de l’argent à quelqu’un, il faut en faire la requête à la banque, puisque c’est elle qui tient les comptes. On parle d’organisme centralisé.
La centralisation a de nombreux avantages, notamment celui d’introduire un tiers de confiance auquel on peut se rapporter en cas de litige, mais elle a également beaucoup de défauts. Entre autres, la concentration de donnée réduit la sécurité du système et entraine une concentration de pouvoir. Dans le cas des banques, l’opacité du système a rendu méfiant de nombreux utilisateurs, notamment à la suite de la crise de 2008. C’est dans ce contexte qu’est née l’idée Bitcoin.
Le principe fondamental de Bitcoin est relativement simple : au lieu que le registre soit maintenu par un seul organisme privé, il est maintenu de manière décentralisée. En clair, chaque ordinateur du réseau (appelé noeud) contient une copie du registre et aide à le maintenir à jour. Dès qu’un noeud reçoit une transaction (ou plutôt, comme nous le verrons par la suite, un bloc de transactions), il la relaie au noeud suivant, puis valide la transaction et met à jour le registre. Le registre est protégé par cette décentralisation : un ou plusieurs noeuds peuvent être altérés ou détruits, le registre sera conservé tant que subsistera au moins un noeud honnête.
Une image souvent utilisée pour représenter la blockchain est celle d’un grand livre des comptes public, infalsifiable et indestructible. Mais ce système est-il vraiment infaillible ? Eh bien, pas vraiment… La décentralisation implique de nombreux challenges techniques plus ou moins évidents à surmonter.
Le challenge principal d’un réseau décentralisé est de s’accorder sur la validité des transactions. Valider une transaction est un processus à plusieurs niveaux : il faut (I) identifier l’émetteur comme légitime (rappelons que tout utilisateur de Bitcoin interagit avec le réseau de manière anonyme), (II) vérifier qu’il possède suffisamment de fond pour effectuer la transaction et (III) ordonner chronologiquement les transactions.
Chaque noeud peut vérifier indépendamment ces conditions assez facilement mais, à l’échelle du réseau, il est beaucoup plus compliqué de trouver un consensus. En effet, n’importe quelle personne possédant un ordinateur peut se connecter de façon anonyme et participer au maintien du registre, ce qui implique qu’un noeud ne peut à priori pas faire confiance aux autres. Permettre à un système décentralisé de s’accorder sans que les participants aient besoin de se faire confiance est, en somme, ce que permet de faire la technologie blockchain.
Plan de l’article
I. Identifier l’émetteur comme légitime
I.1. La paire clé privée/ clé publique
I.2. De l’immense diversité des adresses
I.3. Multisignature : un mécanisme bien pratique
I.4. Protéger sa clé privée
II. UTXOs, ou comment s’assurer que l’émetteur possède bien les fonds suffisants
III. Ordonner chronologiquement les transactions à l’échelle du réseau : la blockchain
III.1. Modèle sans consensus
III.2. Les bases de la Blockchain
III.3. Preuve de travail (PoW)
III.4. Temps de latence
III.5. Nouvelle règle, nouveaux problèmes
III.6. Des noeuds et des arbres
Nb : Dans le début de cet article, nous considèrerons le client (i.e. le programme utilisé pour produire des transactions) comme un noeud à part entière.
I. Identifier l’émetteur comme légitime
I.1. La paire clé privée/ clé publique
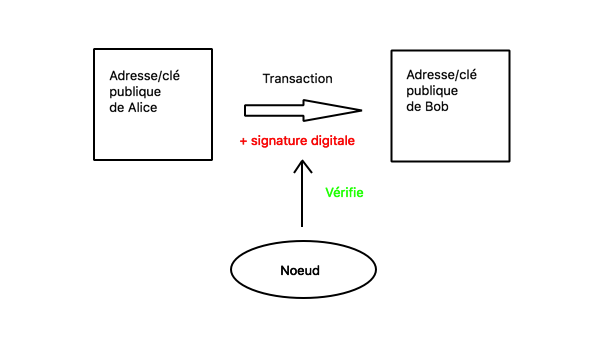
En théorie, lorsqu’un noeud reçoit une transaction transférant une certaine somme de Alice à Bob, il n’a aucun moyen de savoir si Alice est bien l’émetteur de cette transaction.
Pour résoudre ce problème, Bitcoin utilise un système courant en cryptographie basé sur une combinaison clé privée/clé publique. La clé publique, ou adresse, est visible par tous (ndlr: par souci de simplification, nous ferons à ce stade la confusion clé publique/adresse). En pratique, lorsque Alice initie une transaction à destination de Bob, c’est à son adresse qu’elle envoie l’argent.
Cette adresse est directement reliée à la clé privée de Bob, qui est en quelques sorte le mot de passe associé à cette clé. À vrai dire, l’adresse est générée à partir de la clé privée grâce à de complexes fonctions mathématiques dont il suffit de retenir qu’elles fonctionnent à sens unique. Ainsi, en appliquant ces fonctions à une clé privé (P), on obtiendra toujours la même adresse (A), mais il n’est pas possible, connaissant (A), de retrouver (P). Le possesseur de (P) peut donc facilement prouver qu’il possède bien les fonds stockés à l’adresse (A).
Le problème est-il résolu ? Pas encore. Il faut bien comprendre que le système Bitcoin fonctionne de manière décentralisée. Cela implique que vous ne pouvez pas simplement donner votre clé privée au réseau pour prouver que vous possédez les fonds, comme vous donneriez votre mot de passe à une banque en ligne. En effet, un noeud qui recevrait votre clé privée serait en mesure de la réutiliser pour dépenser votre argent (de même que la banque en ligne pourrait en théorie dépenser vos fonds, puisqu’elle connait votre mot de passe). Il est donc nécessaire de trouver un moyen de prouver au réseau que l’on possède la clé privée, sans fournir la clé elle-même. Cette preuve, c’est la signature digitale.
L’idée est simple : au lieu de fournir au réseau la clé privée, on fournit une signature digitale générée à partir de la clé privée et de la transaction considérée. La signature digitale est une preuve que l’émetteur possédait bien la clé privée associée à l’adresse d’émission au moment où il a initié la transaction. Cette signature est passée avec la transaction au réseau, ce qui permet à chaque noeud de valider cette dernière sans avoir accès à la clé privée de l’émetteur.
Cette idée est bien sympathique, mais n’a-t-on pas simplement déplacé le problème ? Le noeud ne peut-il pas réutiliser une signature pour valider une autre transaction depuis la même adresse ?
Non. Cette fois-ci, ce n’est pas possible. En effet, une signature digitale est différente à chaque transaction émise, de telle sorte qu’il est impossible de prendre la signature digitale d’une transaction pour tenter de valider une autre transaction. Pour y voir un peu plus clair, intéressons nous de plus près à l’algorithme de vérification d’une transaction (ndlr : ce qui suit est une vulgarisation de https://en.wikipedia.org/wiki/Elliptic_Curve_Digital_Signature_Algorithm).
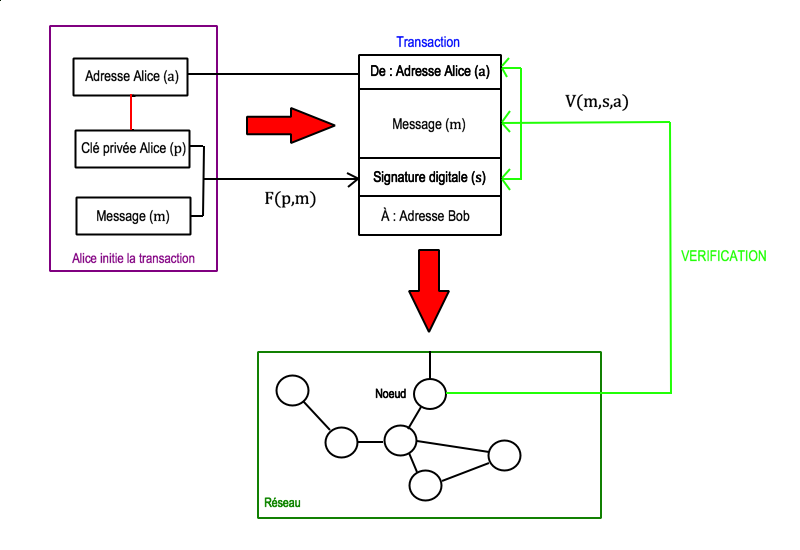
De manière synthétique, la signature digitale est une fonction F prenant en paramètre la clé privée de l’émetteur (p) et le message émis (m). Pour vérifier si la signature est valide, chaque noeud applique une autre fonction V prenant en paramètre l’adresse publique de l’émetteur (a), le message (m) et la signature digitale (s), et qui renvoie vrai ou faux. Il est important de noter que la fonction F est à sens unique, de sorte qu’il est impossible de deviner la clé privée à partir de la signature. Cela implique également une interdépendance entre la signature et le message : F donnera une toujours la même signature pour un message et une clé privée donnés, mais le moindre changement de l’un des deux paramètres aura pour effet d’altérer radicalement la signature. Ainsi, une signature digitale ne pourra jamais être réutilisée. Cela empêche également les noeuds qui relaient la transaction de la modifier au passage. En effet, si l’intégrité du message est corrompue (m devient m’), V renverra faux car le message en entrée n’est plus le même que celui qui avait été passé en paramètre de F.
NB : sur le schéma de la transaction, l’adresse du destinataire apparait distincte du message. En réalité, on peut considérer qu’elle est inclue dans m, de telle sorte qu’un noeud ne puisse pas la modifier sans invalider la signature
I.2. De l’immense diversité des adresses
Jusqu’ici, nous avons fait la confusion clé publique/adresse. Rigoureusement parlant, ces deux termes ne désignent pas exactement la même chose, bien qu’ils remplissent la même fonction. Simplement, une adresse est une version digeste de la clé publique, adaptée à l’utilisation par des humains (comprendre plus courte et plus lisible). Pour obtenir une adresse, il suffit d’appliquer quelques transformations mathématiques à la clé publique, et le tour est joué !
Autre précision importante : lorsque vous créez une paire clé privée/clé publique, vous la créez indépendamment du réseau. En d’autres termes, le réseau ne parcourt pas la liste des adresses déjà utilisées pour vous en proposer une « valide ». Pourquoi ?
La raison se trouve dans le mécanisme de génération d’une adresse. Une adresse est, comme on l’a vu, générée à partir d’une clé publique, qui est elle-même générée à partir d’une clé privée. Ainsi, pour fournir une adresse non utilisée, le réseau devrait générer une clé privée ! Si vous avez bien saisi le principe d’un système décentralisé, vous comprenez donc pourquoi il est impensable que cela fonctionne de cette façon (on ne donne JAMAIS sa clé privée au réseau).
Mais alors, est-il possible que deux personnes génèrent la même paire clé privée/clé publique ? En théorie, oui. Dans ce cas, les deux personnes auraient accès aux fonds stockés à l’adresse correspondante. Rassurez vous cependant, la probabilité que votre clé privée aléatoirement générée donne une adresse déjà utilisée est quasiment nulle.
Pour vous en convaincre, voici un nombre très grand : 2160. Ce nombre représente le nombre total d’adresse Bitcoin possible. En comparaison, il y a environ 263 grains de sable sur terre. Si chacun de ces grains contenait une Terre avec autant de grain de sable, le nombre total de grain de sable serait de 2126, ce qui est encore très inférieur à 2160.
Il est donc mathématiquement impossible (enfin, presque !) que quelqu’un génère une clé privée donnant une adresse déjà utilisée.
Allons encore plus loin, serait-il possible qu’un ordinateur génère des milliers de clés privées, vérifie si l’adresse correspondante a une balance non nulle et, le cas échéant, vire les fonds sur sa propre adresse ? Encore une fois, cette attaque, sans être complètement impossible, est très difficilement réalisable.
Pour s’en convaincre, simplifions le problème et imaginons qu’un programmeur malicieux souhaite trouver la clé privée associée à une adresse spécifique. Supposons que ce programmeur possède un ordinateur capable de générer un milliard (~230) de clés privées par seconde. Il lui faudrait alors en moyenne 2130 secondes pour trouver la bonne clé. Supposons maintenant qu’il possède 1 milliard de milliards de ces ordinateurs, il ne lui faudrait alors plus « que » 270 secondes, ou 245 années. Sachant que l’univers est âgé de 234 années, il ferait mieux de s’y mettre maintenant !
I.3. Multisignature : un mécanisme bien pratique
Jusqu’ici, chacune des adresses que nous avons vues est contrôlée par une unique clé privée. Cependant, il s’est rapidement avéré qu’il serait bien pratique qu’une adresse puisse être contrôlée par plusieurs personnes. Pour ce faire, on a recourt à un mécanisme appelé multisignature, permettant d’effectuer des « m-parmi-n » transactions, où « m » fait référence au nombre de signataires nécéssaire parmi les « n » possesseurs de l’adresse pour débloquer les fonds.
Par exemple, un couple souhaitant avoir une adresse commune utiliserait des « 2-parmi-2 » transactions. Pour autoriser une transaction, il faudrait que les deux conjoints la signent.
Un autre cas envisageable est celui d’une entreprise. Considérons l’exemple suivant : une entreprise souhaite placer les fonds qu’elle utilise pour ses dépenses courantes à une adresse Bitcoin administrée par un bureau de 10 personnes. Une stratégie envisageable serait de créer une « 6-parmi-10 » adresse. La majorité des voix serait alors requise pour dépenser les fonds.
Le mécanisme de création d’une « m-parmi-n » adresse peut être formalisé comme suit :
- Les n parties prenantes génèrent une paire clé privée/clé publique (on a donc n paires)
- À partir des n clé publique, générer une « m-parmi-n » adresse grâce à une fonction spéciale addmultisigaddress
I.4. Protéger sa clé privé
Si vous avez bien suivi, vous devez avoir compris à quel point votre clé privée est précieuse. Si vous l’égarez, personne ne sera en mesure de la retrouver, et les fonds associés à l’adresse correspondante seront définitivement perdus.
Le système de mulltisignature peut être utilisé pour protéger une clé privée (ou plutôt les fonds disponibles à une adresse). Par exemple, vous pourriez créer une « 2-parmi-3 » adresse, garder l’une des clés en votre possession, confier la seconde à un tiers de confiance (comme une banque) et conserver la dernière en lieu sûr. Pour effectuer une transaction, vous auriez à envoyer une requête au tiers de confiance, qui fournirait la deuxième signature requise (la première étant celle de la clé en votre possession) en échange d’une preuve d’identité. Dans le cas où vous perdriez votre clé, il suffirait de récupérer celle stockée en lieu sûr pour avoir accès aux fonds.
Bien évidemment, il est possible d’augmenter le nombre de clés pour baisser la probabilité de perdre l’accès à votre argent (« 2-parmi-4 », « 2-parmi-5 »), mais cela se fait au détriment de la sécurité de votre adresse. En effet, plus il y a de clés, plus la probabilité que quelqu’un mette la main sur au moins deux d’entre elles est importante. Tout est affaire de compromis…
En pratique, très peu de wallet permettent une protection via multi-signature. C’est pourquoi il est primordial de sauvegarder (backup) sa clé privée dans plusieurs endroits sûrs. Entre autres, vous pouvez garder une copie sur votre ordinateur, une dans une clé usb et une imprimée sur papier (ce n’est pas un conseil, juste un exemple).
Dernière petite précision, concernant Ethereum cette fois. Les wallet Ethereum vous demandent généralement un mot de passe pour générer une paire clé privée/clé publique. Cela ajoute un niveau de sécurité à votre compte : si quelqu’un obtenait votre clé privée (encryptée avec votre mot de passe), il ne pourrait pas accéder à vos fonds sans ce mot de passe.
Certains wallet comme MyEtherWallet vous fournissent votre clé privée non encryptée. Bien que plus facile à utiliser (pas besoin de taper le mot de passe), elle est également plus vulnérable, donc faites bien attention !
Dans tous les cas, n’oubliez pas de sauvegarder votre clé privée ET votre mot de passe ! Pour plus d’informations : https://www.ethereum-france.com/creer-et-gerer-son-portefeuille-dether-en-2-minutes-avec-myetherwallet-com/.
II. UTXOs, ou comment s’assurer que l’émetteur possède suffisamment de fonds
Contrairement aux banques traditionnelles (et à Ethereum !), le registre maintenu par le réseau de noeuds ne contient pas la balance associée à chaque adresse.
Pour calculer la balance d’un compte (NB : on définit par compte une paire clé privée/clé publique), un noeud fait la somme des « sorties de transaction non dépensées » (Unspent Transaction Output ou UTXO) associées à l’adresse du compte considéré.
Derrière ce nom barbare se cache une réalité relativement simple : pour justifier sa validité, toute transaction référence en entrée une ou plusieurs transactions passées dont la somme des sorties est supérieure ou égale à son montant. Ce mécanisme de référencement entraine la formation d’une chaine de transaction.
La chaîne de transaction a une propriété fondamentale : une transaction peut référencer de multiples UTXOs en entrée et en sortie, mais un UTXO spécifique ne peux être utilisé qu’une fois en tant qu’entrée. Cela permet d’empêcher que la même somme d’argent ne soit dépensée deux fois.
Les UTXOs sont stockés dans une base de données dont chaque noeud possède une copie. À chaque transaction validée, la base de données est mise à jour.
Pour mieux comprendre, considérons l’exemple suivant. Supposons que Alice souhaite envoyer 15 BTC à Bob. Pour ce faire, elle doit, lors de l’initiation de la transaction, renseigner en entrée une ou plusieurs transactions lui ayant été adressées, dont les sorties n’ont pas été dépensées et dont la valeur totale est supérieure ou égale à 15 BTC.
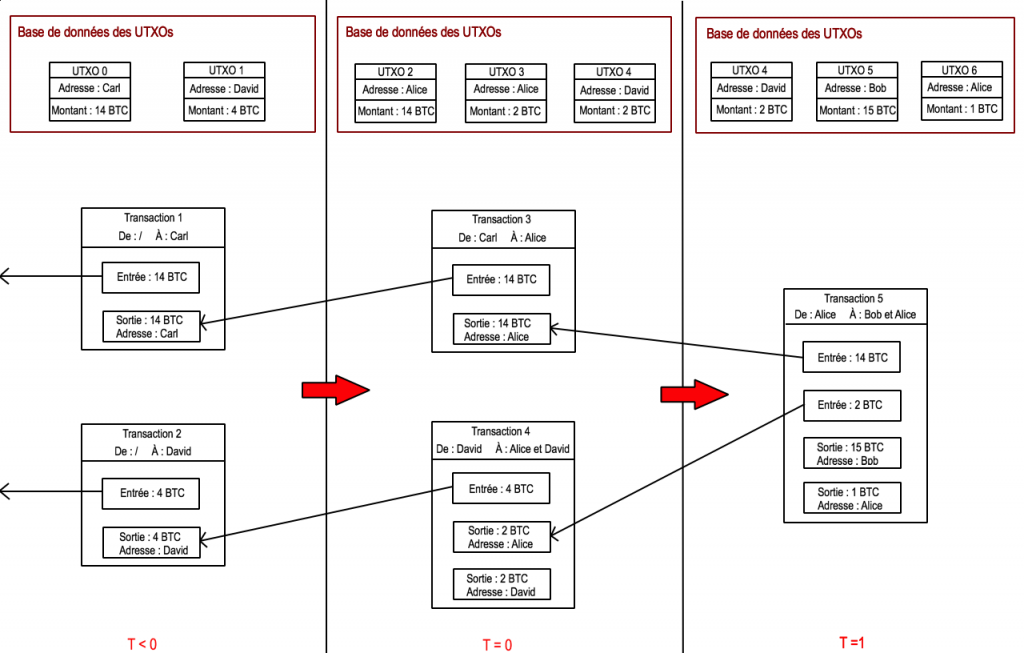
Le schéma ci-après illustre de manière très simplifiée le fonctionnement de la chaîne de transaction ayant amenée à cette opération. On suppose qu’à T<0 la base de données des UTXOs ne contient que deux UTXOs, l’un de valeur 14 BTC, affecté à l’adresse de Carl, et l’autre de valeur 4 BTC, affecté à l’adresse de David. À T=0, Carl et David effectuent une transaction à destination de Alice puis, à T=1, Alice effectue une transaction à destination de Bob.
Comme indiqué sur le schéma, toute transaction doit indiquer une ou plusieurs entrées, chacune référençant une sortie de transaction non dépensée (c’est à dire présente dans la base de données des UTXOs) et dont l’adresse correspond à l’adresse de l’émetteur. Pour pouvoir utiliser cet UTXO, il faut que l’émetteur fournisse une signature digitale qui prouve qu’il possède bien la clé privée associée à l’adresse de l’UTXO.
Notez aussi que pour chaque transaction, la somme des entrées est égale à la somme des sorties. Par exemple, pour la transaction 5, Alice souhaite envoyer 15 BTC à Bob. Elle doit donc référencer des UTXOs dont la somme des montants est supérieur ou égale à 15 BTC. Il est important de bien comprendre que les UTXOs ne sont pas divisibles. Alice doit donc utiliser ses 2 UTXOs, dont la valeur totale est de 16 BTC. Pour récupérer le change de 1 BTC, Alice « crée » une sortie de 1 BTC affectée à son adresse. Alors, la base de données des UTXOs ajoute un UTXO de valeur 1 BTC, que Alice sera en mesure d’utiliser plus tard.
Dans le cas où la somme des entrées n’est pas égale à la somme des sorties, la différence (Total sortie – Total entrée) est considérée comme un frais de transaction et peut être affectée au mineur de la transaction (nous verrons ce que cela signifie un peu plus tard).
Bien entendu, la chaine de transaction Bitcoin est en pratique beaucoup plus massive que celle présentée ci-dessus. Lorsqu’un noeud se connecte au réseau pour la première fois, il doit constituer sa base de données des UTXOs. Pour ce faire, il parcourt l’ensemble de toutes les transactions jamais effectuées et enregistre dans la base toute sortie de transaction non dépensée. Ce processus est long, il peut prendre jusqu’à plusieurs heures, mais n’a besoin d’être effectué qu’une seule fois. Après, un noeud synchronise sa base de données en temps réel.
À ce stade, il nous reste une question à éclaircir : d’où vient l’argent ? En effet, si pour dépenser des Bitcoin il faut référencer une ou plusieurs transactions où l’on a reçu au moins autant de Bitcoin, comment ces Bitcoin sont-il apparus à l’origine ? En réalité, la création de Bitcoin est en lien étroit avec le système de blockchain et de Mining. Nous verrons tout cela en détails dans très peu de temps. Pour l’instant, retenez simplement que des bitcoin « sortis de nul part » peuvent être attribués à certains noeuds à certains moments de la vie de la blockchain.
Nous pouvons désormais exprimer en paradigme le mécanisme de validation d’une transaction par un noeud :
- Pour chaque entrée dans la transaction :
– Si l’UTXO référencé n’est pas dans la base de données des UTXOs, retourner une erreur
– Si la signature fournie ne correspond pas à celle du propriétaire de l’UTXO (i.e. pas la même adresse), retourner une erreur - Si la somme des montants des UTXOs référencés en entrée n’est pas égale à la somme des montants des UTXOs en sortie, retourner une erreur
- Mettre à jour la base de données des UTXOs
Et voilà, vous savez désormais comment les transactions sont validées ! Nous allons maintenant pouvoir aborder le fonctionnement de la blockchain en toute sérénité !