FAQ sur le Proto-Danksharding

Après la mise à jour Shapella, qui avait permis les retraits du staking, la prochaine évolution majeure du réseau Ethereum sera intitulé Cancun-Deneb. Prévue pour le début de l'année 2024, cette mise à jour apportera d'importantes avancées, notamment l'implémentation du proto-danksharding via l'EIP-4844, ainsi que plusieurs EIP de moindre envergure. Cette traduction en français d'une FAQ de Vitalik vous propose de plonger dans les discussions techniques autour du proto-danksharding : bonne lecture !

Danksharding est le nouveau design de sharding proposé pour Ethereum, qui introduit des simplifications significatives par rapport aux conceptions précédentes.

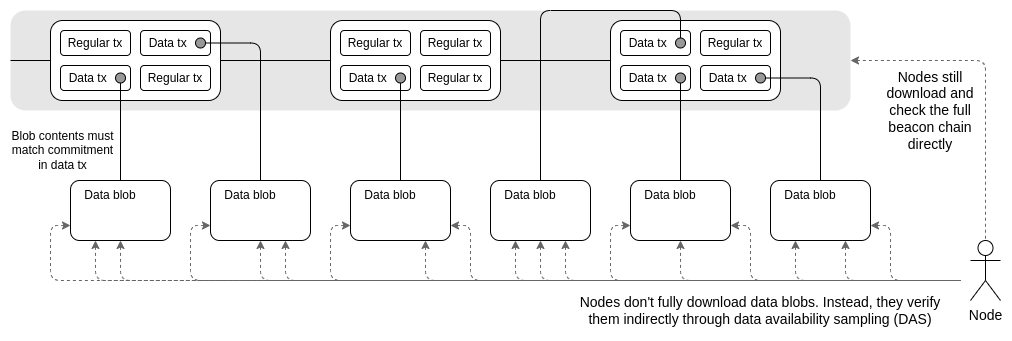
La principale différence entre toutes les propositions récentes de sharding d'Ethereum depuis ~2020 (à la fois Danksharding et pré-Danksharding) et la plupart des propositions de sharding non-Ethereum est la feuille de route centrée sur les rollups d'Ethereum : au lieu de fournir plus d'espace pour les transactions, le sharding d'Ethereum offre plus d'espace pour des "blobs" de données, que le protocole Ethereum lui-même ne tente pas d'interpréter. Vérifier un "blob" nécessite simplement de s'assurer que le "blob" est disponible — c’est-à-dire qu'il peut être téléchargé depuis le réseau. L'espace de données dans ces "blobs" est censé être utilisé par les protocoles de rollup de deuxième couche qui prennent en charge des transactions à haut débit.

La principale innovation introduite par Danksharding est le marché des frais fusionné : au lieu d'avoir un nombre fixe de shards ayant chacun des blocs distincts et des proposants de blocs distincts, dans Danksharding, il n'y a qu'un seul proposant qui choisit toutes les transactions et toutes les données qui entrent dans cet emplacement.
Pour éviter que ce design n'impose des exigences système élevées aux validateurs, nous introduisons la séparation des rôles entre le proposant et le constructeur (= Proposer Builder Separation PBS). Une classe spécialisée d'acteurs appelés constructeurs de blocs enchérissent pour avoir le droit de choisir le contenu du slot, et le proposant n'a qu'à sélectionner l'en-tête valide avec l'enchère la plus élevée. Seul le constructeur de bloc doit traiter l'ensemble du bloc (et même là, il est possible d'utiliser des protocoles d'oracles décentralisés tiers pour mettre en œuvre un constructeur de bloc distribué) ; tous les autres validateurs et utilisateurs peuvent vérifier les blocs très efficacement grâce à l'échantillonnage de la disponibilité des données (rappelez-vous : la partie "grande" du bloc est simplement des données).

Le proto-danksharding, également connu sous le nom d'EIP-4844, est une proposition visant à mettre en œuvre la majeure partie de la logique et de la "structure" (par exemple, les formats de transaction, les règles de vérification) qui constituent une spécification complète de Danksharding, sans encore implémenter effectivement de sharding. Dans une implémentation proto-danksharding, tous les validateurs et utilisateurs doivent toujours valider directement la disponibilité de l'ensemble des données.

La principale caractéristique introduite par le proto-danksharding est un nouveau type de transaction que nous appelons une transaction porteuse de "blob". Une transaction porteuse de "blob" est similaire à une transaction régulière, sauf qu'elle transporte également une pièce de données supplémentaire appelée un "blob". Les "blobs" sont extrêmement volumineux (~125 ko) et peuvent être beaucoup moins coûteux que des quantités similaires de calldata. Cependant, les données du "blob" ne sont pas accessibles à l'exécution de l'EVM ; l'EVM peut seulement voir un engagement envers le "blob".

Cela concerne la différence entre la charge moyenne et la charge maximale possible. Aujourd'hui, nous sommes déjà dans une situation où la taille moyenne des blocs est d'environ 90 ko, mais la taille maximale théorique possible d'un bloc (si les 30 millions de gaz dans un bloc étaient utilisés pour les données d'appel) est d'environ 1,8 Mo. Le réseau Ethereum a géré par le passé des blocs approchant de la charge maximale. Cependant, si nous réduisons simplement le coût en gaz des données d'appel de 10 fois, alors même si la taille moyenne des blocs augmenterait à des niveaux encore acceptables, le pire des cas atteindrait 18 Mo, ce qui est bien trop élevé pour que le réseau Ethereum puisse le gérer.

Le schéma actuel de tarification du gaz rend impossible de séparer ces deux facteurs : le rapport entre la charge moyenne et la charge maximale est déterminé par les choix des utilisateurs concernant la quantité de gaz qu'ils dépensent pour les données d'appel par rapport à d'autres ressources. Cela signifie que les prix du gaz doivent être fixés en fonction des possibilités du pire des cas, entraînant une charge moyenne inutilement inférieure à ce que le système peut gérer. Mais si nous modifions la tarification du gaz pour créer plus explicitement un marché des frais multidimensionnel, nous pouvons éviter le déséquilibre entre la charge moyenne et le scénario catastrophe, et inclure dans chaque bloc une quantité proche du maximum de données que nous pouvons gérer en toute sécurité. Proto-danksharding et EIP-4488 sont deux propositions qui font exactement cela.

	Charge moyenne d’un bloc	Pire scénario d’un bloc
Status quo	85 kb	1.8 mb
EIP-4488	Inconnu, 350 kb si 5 fois plus d’utilisation de calldata	1.4 mb
Proto-danksharding	1 mb (ajustable si souhaité)	2 mb

L'EIP-4488 est une tentative antérieure et plus simple de résoudre le même problème de déséquilibre entre la charge moyenne et le scénario catastrophe. L'EIP-4488 a accompli cela avec deux règles simples :

La réduction du coût en gaz des données d'appel de 16 gaz par octet à 3 gaz par octet.
Une limite de 1 Mo par bloc plus 300 octets supplémentaires par transaction (maximum théorique : ~1,4 Mo).

La limite stricte est la manière la plus simple d'assurer que l'augmentation plus importante de la charge moyenne n'entraîne pas également une augmentation de la charge du scénario catastrophe. La réduction du coût en gaz augmenterait considérablement l'utilisation des rollups, augmentant probablement la taille moyenne des blocs à plusieurs centaines de kilo octets, mais la possibilité du scénario catastrophe de blocs uniques contenant 10 Mo serait directement empêchée par la limite stricte. En fait, la taille du bloc dans le pire des cas serait inférieure à celle d'aujourd'hui (1,4 Mo contre 1,8 Mo).

Proto-danksharding crée plutôt un type de transaction distinct qui peut contenir des données moins coûteuses dans de gros blobs de taille fixe, avec une limite sur le nombre de blobs pouvant être inclus par bloc. Ces blobs ne sont pas accessibles depuis l'EVM (seuls les engagements envers les blobs le sont), et les blobs sont stockés par la couche de consensus au lieu de la couche d'exécution.

La principale différence pratique entre l'EIP-4488 et le proto-danksharding est que l'EIP-4488 tente de minimiser les changements nécessaires aujourd'hui, tandis que le proto-danksharding apporte un plus grand nombre de changements aujourd'hui afin de réduire le nombre de changements nécessaires à l'avenir pour passer à un sharding complet. Bien que la mise en œuvre d'un sharding complet (avec un échantillonnage de la disponibilité des données, etc.) soit une tâche complexe et reste une tâche complexe même après le proto-danksharding, cette complexité est contenue dans la couche de consensus. Une fois que le proto-danksharding est déployé, les équipes clientes de la couche d'exécution, les développeurs de rollup et les utilisateurs n'ont plus besoin de faire aucun travail supplémentaire pour terminer la transition vers un sharding complet. Le proto-danksharding sépare également les données des blobs des données d'appel, facilitant ainsi le stockage des données des blobs pendant une période plus courte par les clients.

Il est important de noter que le choix entre les deux n'est pas exclusif : nous pourrions mettre en œuvre l'EIP-4488 bientôt, puis la suivre avec le proto-danksharding six mois plus tard.

Citons l'EIP-4844 :

Le travail déjà accompli dans cette EIP comprend :

Un nouveau type de transaction, exactement du même format qui devra exister dans un "sharding complet".
Toute la logique de la couche d'exécution requise pour un sharding complet.
Toute la logique de vérification croisée entre l'exécution et le consensus requise pour un sharding complet.
Une séparation des couches entre la vérification de “BeaconBlock” et l'échantillonnage de disponibilité des données des blocs.
La majeure partie de la logique “BeaconBlock” requise pour un sharding complet.
Un ajustement automatique du prix du gaz indépendant pour les blocs de données.

Le travail qui reste à faire pour parvenir à un sharding complet comprend :

Une extension à faible degré des “blob_kzgs” dans la couche de consensus pour permettre un échantillonnage en 2D.
Une implémentation réelle de l'échantillonnage de disponibilité des données.
PBS (séparation des rôles de proposant et de constructeur) pour éviter de demander à chaque validateur de traiter 32 Mo de données en un seul slot.
Une preuve de garde ou une exigence similaire dans le protocole pour chaque validateur afin de vérifier une partie singulière des données sharded dans chaque bloc.

Tant l’EIP-4488 que le proto-danksharding conduisent à une utilisation maximale à long terme d'environ 1 Mo par slot (12 secondes). Cela équivaut à environ 2,5 To par an, un taux de croissance bien plus élevé que ce qu'Ethereum requiert actuellement.

Dans le cas d'EIP-4488, la résolution de ce problème nécessite l'expiration de l'historique (EIP-4444), où les clients ne sont plus tenus de stocker l'historique plus ancien qu'une certaine durée (des durées de 1 mois à 1 an ont été proposées).

Dans le cas de proto-danksharding, la couche de consensus peut mettre en œuvre une logique distincte pour supprimer automatiquement les données des blobs après un certain temps (par exemple, 30 jours), que l'EIP-4444 soit mise en œuvre ou non. Cependant, il est fortement recommandé de mettre en œuvre l'EIP-4444 dès que possible, quelle que soit la solution de mise à l'échelle des données adoptée à court terme.

Les deux stratégies limitent la charge supplémentaire sur le disque d'un client de consensus à au plus quelques centaines de gigaoctets. À long terme, l'adoption d'un mécanisme d'expiration de l'historique est essentiellement obligatoire : un sharding complet ajouterait environ 40 To de données d'historique de blobs par an, de sorte que les utilisateurs ne pourraient réalistement stocker qu'une petite partie de celles-ci pendant un certain temps. Il est donc utile de définir ces attentes plus tôt.

L'objectif du protocole de consensus d'Ethereum n'est pas de garantir le stockage éternel de toutes les données historiques. Au contraire, l'objectif est de fournir un tableau d'affichage en temps réel hautement sécurisé et de laisser de la place à d'autres protocoles décentralisés pour assurer le stockage à plus long terme. Le tableau d'affichage (= bulltin board) est là pour s'assurer que les données publiées restent disponibles suffisamment longtemps pour que tout utilisateur qui souhaite ces données, ou tout protocole à plus long terme sauvegardant les données, ait amplement de temps pour récupérer les données et les importer dans leur autre application ou protocole.

En général, le stockage historique à long terme est facile. Alors que demander 2,5 To par an peut être trop pour les nœuds réguliers, c'est tout à fait gérable pour les utilisateurs dédiés : on peut acheter des disques durs très volumineux pour environ 20 $ par téraoctet, bien à la portée d'un passionné. Contrairement au consensus, qui repose sur un modèle de confiance N/2-sur-N, le stockage historique suit un modèle de confiance 1-sur-N : vous avez seulement besoin qu'un des conservateurs des données soit honnête. Par conséquent, chaque morceau de données historiques doit seulement être stocké des centaines de fois, et non pas par l'ensemble complet des milliers de nœuds qui effectuent une vérification de consensus en temps réel.

Quelques moyens pratiques par lesquels l'ensemble de l'historique sera stocké et rendu facilement accessible comprennent :

Les protocoles spécifiques à une application (par exemple, les rollups) peuvent exiger que leurs nœuds stockent la partie de l'historique qui est pertinente pour leur application. La perte de données historiques n'est pas un risque pour le protocole, seulement pour les applications individuelles, il est donc logique que les applications assument la charge de stocker des données qui leur sont pertinentes.
Stocker les données historiques dans BitTorrent, par exemple, en générant automatiquement et en distribuant un fichier de 7 Go contenant les données de blocs de chaque jour.
Le réseau Ethereum Portal (actuellement en développement) peut facilement être étendu pour stocker l'historique.
Les explorateurs de blocs, les fournisseurs d'API et d'autres services de données stockeront probablement l'historique complet.
Les passionnés individuels et les universitaires effectuant des analyses de données stockeront probablement l'historique complet. Dans ce dernier cas, le stockage local de l'historique leur procure une valeur significative car il facilite beaucoup les calculs directs sur ces données.
Les protocoles d'indexation tiers tels que TheGraph stockeront probablement l'historique complet.

Un blob est un vecteur de 4096 éléments de champ, des nombres dans la plage :

0 <= x < 5243587517512619047944774
05081859658376905525005276
37822603658699938581184513

Mathématiquement, le blob est traité comme représentant un polynôme de degré < 4096 sur le corps fini avec le modulo mentionné ci-dessus, où l'élément de champ à la position ii dans le blob est l'évaluation de ce polynôme en ω^i. ω est une constante qui satisfait ω^4096=1.

Un engagement envers un blob est un hachage de l'engagement KZG pour le polynôme. Du point de vue de l'implémentation, cependant, il n'est pas important de se préoccuper des détails mathématiques du polynôme. Au lieu de cela, il y aura simplement un vecteur de points de courbe elliptique (la configuration de confiance basée sur la base de Lagrange), et l'engagement KZG envers un blob sera simplement une combinaison linéaire.

Citons le code de l'EIP-4844 :

def blob_to_kzg(blob: Vector[BLSFieldElement, 4096]) -> KZGCommitment:

computed_kzg = bls.Z1

for value, point_kzg in zip(tx.blob, KZG_SETUP_LAGRANGE):

assert value < BLS_MODULUS

computed_kzg = bls.add(

computed_kzg,

bls.multiply(point_kzg, value)

)

return computed_kzg

BLS_MODULUS est le modulo mentionné ci-dessus, et KZG_SETUP_LAGRANGE est le vecteur de points de courbe elliptique qui constitue la configuration de confiance basée sur la base de Lagrange. Pour les implémentateurs, il est raisonnable de simplement considérer cela pour le moment comme une fonction de hachage spéciale à usage particulier.

Au lieu d'utiliser le KZG pour représenter directement le blob, l'EIP-4844 utilise le hachage versionné : un seul octet 0x01 (représentant la version), suivi des 31 derniers octets du hachage SHA256 du KZG.

Cela est fait pour la compatibilité avec l'EVM (Ethereum Virtual Machine) et la compatibilité future : les engagements KZG font 48 octets tandis que l'EVM fonctionne de manière plus naturelle avec des valeurs de 32 octets, et si nous passons un jour de KZG à quelque chose d'autre (par exemple, pour des raisons de résistance quantique), les engagements peuvent continuer à faire 32 octets.

Le proto-danksharding introduit deux précompilations : la précompilation de vérification de blob et la précompilation d'évaluation de point.

La précompilation de vérification de blob est explicite : elle prend en entrée un hachage versionné et un blob, et vérifie que le hachage versionné fourni est effectivement un hachage versionné valide pour le blob. Cette précompilation est destinée à être utilisée par les rollups optimistes. Citons l'EIP-4844 :

Les rollups optimistes n'ont besoin de fournir les données sous-jacentes que lors de la soumission de preuves de fraude. La fonction de soumission de preuve de fraude nécessiterait que le contenu complet du blob frauduleux soit soumis en tant que partie de calldata. Elle utiliserait la fonction de vérification de blob pour vérifier les données par rapport au hachage versionné qui a été soumis auparavant, puis effectuerait la vérification de la preuve de fraude sur ces données, comme cela se fait aujourd'hui.

La précompilation d'évaluation de point prend en entrée un hachage versionné, une coordonnée x, une coordonnée y et une preuve (l'engagement KZG du blob et une preuve d'évaluation KZG). Elle vérifie la preuve pour vérifier que P(x)=y, où P est le polynôme représenté par le blob qui a le hachage versionné donné. Cette précompilation est destinée à être utilisée par les rollups ZK. Citons l'EIP-4844 :

Les rollups ZK fourniraient deux engagements pour leurs données de transaction ou de delta d'état : le kzg dans le blob et un engagement utilisant le système de preuve interne du rollup ZK. Ils utiliseraient un protocole de preuve d'équivalence d'engagement, en utilisant la précompilation d'évaluation de point, pour prouver que le kzg (que le protocole garantit pointer vers des données disponibles) et l'engagement propre au rollup ZK se réfèrent aux mêmes données.

Supposons que K soit l'engagement KZG et B soit le blob auquel il s'engage. Tous les protocoles ZK-SNARK ont une manière d'importer de grandes quantités de données dans une preuve et contiennent une sorte d'engagement envers ces données. Par exemple, dans PLONK, il s'agit de l'engagement QC.

Tout ce que nous avons à faire est de prouver que K et QC s'engagent aux mêmes données. Cela peut être fait avec une preuve d'équivalence, qui est très simple. Citons le post :

Supposons que vous ayez plusieurs engagements polynomiaux C1,…,CkC1,…,Ck, sous k différents schémas d'engagements (par exemple, Kate, FRI, quelque chose basé sur Bulletproofs, DARK...), et que vous vouliez prouver qu'ils s'engagent tous au même polynôme P.

Nous pouvons prouver cela facilement :

Posons z=hash(C1,…,Ck), où nous interprétons z comme un point d'évaluation auquel P peut être évalué.

Publions les ouvertures O1,…,Ok où Oi est une preuve que Ci(z)=a sous le i-ème schéma d'engagement. Vérifions que a est le même nombre dans tous les cas.

Une transaction de ZK rollup aurait simplement à avoir un SNARK régulier, ainsi qu'une preuve d'équivalence de ce genre pour prouver que ses données publiques équivalent au hachage versionné. Notez qu'ils ne devraient PAS implémenter la vérification KZG directement ; au lieu de cela, ils devraient simplement utiliser la précompilation d'évaluation de point pour vérifier l'ouverture. Cela garantit la pérennité : si plus tard KZG est remplacé par quelque chose d'autre, le ZK rollup serait en mesure de continuer à fonctionner sans problème supplémentaire.

Si le ZK-SNARK de destination utilise un autre module, ou même n'est pas du tout basé sur des polynômes (par exemple, s'il utilise R1CS), il existe une approche légèrement plus complexe qui peut prouver l'équivalence. La preuve fonctionne comme suit :

Soit P(x) le polynôme encodé par le blob. Faites un engagement Q dans le schéma ZK-SNARK qui encode les valeurs v1,…,vn, où vi=P(ωi).
Choisissez x en hachant l'engagement de P et Q.
Prouvez P(x) avec la précompilation d'évaluation de point.
Utilisez l'équation barycentrique P(x)=xN−11N∑iviωix−ωi pour effectuer la même évaluation à l'intérieur du ZKP. Vérifiez que la réponse est la même que la valeur prouvée en (3).

Dans notre cas particulier, le plan actuel est de lancer simultanément quatre cérémonies (avec des secrets différents) avec des tailles (n1=4096, n2=16), (n1=8192, n2=16), (n1=16384, n2=16) et (n1=32768, n2=16). Théoriquement, seule la première est nécessaire, mais en en lançant davantage avec des tailles plus grandes, nous améliorons la pérennité en nous permettant d'augmenter la taille des blobs.

Nous ne pouvons pas simplement avoir une configuration plus grande, car nous voulons être en mesure d'avoir une limite stricte sur le degré des polynômes qui peuvent être validement engagés, et cette limite est égale à la taille du blob. La manière pratique de le faire serait de commencer avec la configuration de Filecoin, puis de lancer une cérémonie pour l'étendre. Plusieurs mises en œuvre, y compris une mise en œuvre dans un navigateur, permettraient à de nombreuses personnes de participer.

Les engagements non arithmétiques (par exemple, les fonctions de hachage) ne sont pas compatibles avec l'échantillonnage de la disponibilité des données, donc si nous utilisons un tel schéma, nous devrions de toute façon passer à KZG lorsque nous passerons au sharding complet.
Les IPA peuvent être compatibles avec l'échantillonnage de la disponibilité des données, mais cela conduit à un schéma beaucoup plus complexe avec des propriétés beaucoup plus faibles (par exemple, l'auto-guérison et la construction de blocs distribuée deviennent beaucoup plus difficiles).
Ni les hachages ni les IPA ne sont compatibles avec une mise en œuvre bon marché de la précompilation d'évaluation de point. Par conséquent, une mise en œuvre basée sur le hachage ou l'IPA ne pourrait pas bénéficier efficacement aux ZK rollups ou prendre en charge des preuves de fraude bon marché dans des rollups optimistes multi-tours.

Une façon de conserver l'échantillonnage de la disponibilité des données et l'évaluation de point tout en introduisant un autre engagement est de stocker plusieurs engagements (par exemple, KZG et SHA256) par blob. Mais cela engendre des difficultés : soit (i) nous devons ajouter une preuve de ZKP d'équivalence compliquée, soit (ii) tous les nœuds de consensus devraient vérifier le deuxième engagement, ce qui les obligerait à télécharger l'intégralité des données de tous les blobs (des dizaines de mégaoctets par créneau).

Les engagements KZG ont été introduits dans un article en 2010 et ont été largement utilisés depuis environ 2019 dans les protocoles ZK-SNARK de style PLONK. Cependant, les mathématiques sous-jacentes des engagements KZG sont une pièce relativement simple d'arithmétique sur la base des opérations sous-jacentes des courbes elliptiques et des appariements.

La courbe spécifique utilisée est BLS12-381, qui a été générée à partir de la famille Barreto-Lynn-Scott inventée en 2002. Les appariements de courbes elliptiques, nécessaires pour vérifier les engagements KZG, sont des mathématiques très complexes, mais ils ont été inventés dans les années 1940 et appliqués à la cryptographie depuis les années 1990. En 2001, de nombreux algorithmes cryptographiques proposés utilisaient des appariements.

D'un point de vue de la complexité de l'implémentation, KZG n'est pas significativement plus difficile à mettre en œuvre que IPA : la fonction de calcul de l'engagement (voir ci-dessus) est exactement la même que dans le cas de l'IPA, mais avec un ensemble différent de constantes de points de courbe elliptique. La précompilation de vérification des points est plus complexe, car elle implique une évaluation d'appariement, mais les mathématiques sont identiques à une partie de ce qui est déjà fait dans les mises en œuvre de l'EIP-2537 (précompilations BLS12-381) et très similaires à la précompilation d'appariement bn128 (voir aussi : implémentation Python optimisée). Par conséquent, il n'y a pas de "nouveau travail" compliqué requis pour implémenter la vérification KZG.

Il y a quatre composants majeurs.

Les modifications de consensus de la couche d'exécution (voir l'EIP pour plus de détails) :

Un nouveau type de transaction contenant des blobs
Une opcode qui produit le hachage versionné du i-ème blob dans la transaction actuelle
La précompilation de vérification des blobs
La précompilation d'évaluation de points

Les modifications de consensus de la couche de consensus (voir ce dossier dans le dépôt) :

La liste des engagements KZG des blobs dans BeaconBlockBody
Le mécanisme "sidecar", où le contenu complet des blobs est transmis avec un objet distinct du BeaconBlock
Vérification croisée entre les hachages versionnés des blobs dans la couche d'exécution et les engagements KZG des blobs dans la couche de consensus

Notez que pour une implémentation minimale, la mempool n'est pas nécessaire du tout (nous pouvons compter sur des places de marché de regroupement de transactions de deuxième couche à la place), et un seul client doit mettre en œuvre la logique de construction de bloc. Des tests de consensus approfondis ne sont nécessaires que pour les modifications de consensus de la couche d'exécution et de la couche de consensus, qui sont relativement légères. Tout ce qui se situe entre une implémentation minimale et un déploiement "complet" où tous les clients prennent en charge la production de blocs et la mempool est possible.

Proto-danksharding introduit un marché des frais EIP-1559 multidimensionnel, où il y a deux ressources, le gaz et les blobs, avec des prix du gaz flottants distincts et des limites distinctes.

Cela signifie qu'il y a deux variables et quatre constantes :

	Cible par bloc	Max par bloc	Basefee
Gaz	15 million	30 million	Variable
Blob	8	16	Variable

La taxe sur les blobs est prélevée en gaz, mais c'est une quantité variable de gaz qui s'ajuste de sorte que, à long terme, le nombre moyen de blobs par bloc équivaut réellement à la cible.

La nature bidimensionnelle signifie que les constructeurs de blocs vont faire face à un problème plus difficile : au lieu d'accepter simplement les transactions avec les frais de priorité les plus élevés jusqu'à ce qu'ils soient épuisés ou atteignent la limite de gaz du bloc, ils devraient simultanément éviter de toucher deux limites différentes.

Voici un exemple. Supposons que la limite de gaz soit de 70 et que la limite de blobs soit de 40. La mempool a de nombreuses transactions, suffisamment pour remplir le bloc, de deux types (le gaz de tx comprend le gaz par blob) :

Frais de priorité 5 par gaz, 4 blobs, 4 gaz au total
Frais de priorité 3 par gaz, 1 blob, 2 gaz au total

Un mineur qui suit l'algorithme naïf de "suivre les frais de priorité" remplirait tout le bloc avec 10 transactions (40 gaz) du premier type, et obtiendrait un revenu de 5 * 40 = 200. Parce que ces 10 transactions remplissent complètement la limite de blobs, il ne pourrait pas inclure plus de transactions. Mais la stratégie optimale est de prendre 3 transactions du premier type et 28 du deuxième type. Cela donne un bloc avec 40 blobs et 68 gaz, et 5 * 12 + 3 * 56 = 228 revenus.

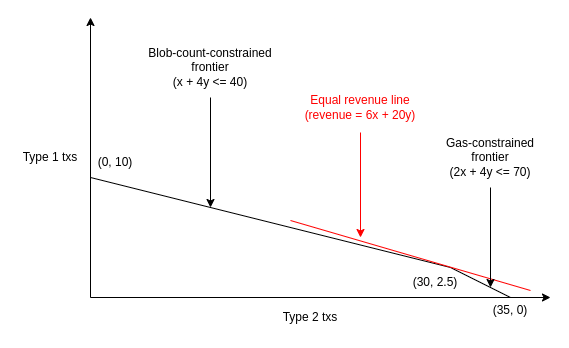
Les clients d'exécution vont-ils devoir mettre en œuvre des algorithmes complexes de problème du sac à dos multidimensionnel pour optimiser leur production de blocs maintenant ? Non, pour quelques raisons :

L'EIP-1559 garantit que la plupart des blocs ne toucheront aucune des limites, donc seulement quelques blocs sont réellement confrontés au problème d'optimisation multidimensionnel. Dans le cas habituel où la mempool n'a pas assez de transactions (payant suffisamment de frais) pour toucher l'une ou l'autre limite, n'importe quel mineur pourrait simplement obtenir le revenu optimal en incluant chaque transaction qu'il voit.
Des heuristiques assez simples peuvent s'approcher de l'optimal en pratique. Consultez l'analyse de l'EIP-4488 d'Ansgar pour certaines données à ce sujet dans un contexte similaire.

La tarification multidimensionnelle n'est même pas la plus grande source de gains, au contraire des revenus provenant de la spécialisation - MEV. Les revenus MEV spécialisés extractibles grâce à des algorithmes spécialisés à partir de l'arbitrage DEX on-chain, des liquidations, du front-running des ventes NFT, etc., représentent une fraction significative du "revenu naïvement extractible" total (c'est-à-dire les frais de priorité) : les revenus MEV spécialisés semblent en moyenne autour de 0,025 ETH par bloc, et les frais de priorité totaux sont généralement autour de 0,1 ETH par bloc.
La séparation du proposant/constructeur est conçue autour du fait que la production de blocs est déjà très spécialisée. PBS transforme le processus de construction de bloc en une enchère, où des acteurs spécialisés peuvent enchérir pour le privilège de créer un bloc. Les validateurs réguliers n'ont qu'à accepter la plus haute enchère. Cela était destiné à empêcher les économies d'échelle entraînées par la MEV de s'infiltrer dans la centralisation des validateurs, mais cela résout tous les problèmes qui pourraient rendre la construction optimale de blocs plus difficile.

L'EIP-1559 d'aujourd'hui ajuste la basefee b pour atteindre un niveau d'utilisation de gaz cible t comme suit :

bn+1=bn⋅(1+u−t8t)

Où bn est la basefee actuelle du bloc, bn+1 est la basefee du prochain bloc, t est la cible et u est le gaz utilisé. L'objectif est que lorsque u>t (donc, l'utilisation est au-dessus de la cible), la basefee augmente, et lorsque u<t, la basefee diminue. Le mécanisme d'ajustement des frais dans proto-danksharding atteint exactement le même objectif de cibler une utilisation moyenne à long terme de t, et il fonctionne de manière très similaire, mais il corrige un bogue subtil dans l'approche de l'EIP-1559.

Supposons, dans l'EIP-1559, que nous ayons deux blocs, le premier avec u=0 et le suivant avec u=2t. Nous obtenons :

Numéro de bloc	Gaz dans le bloc	Basefee
k	-	x
k+1	0	⅞ * x
k+2	2t	⅞ * 9/8 * x = 63/64 * x

Malgré une utilisation moyenne égale à t, la basefee diminue d'un facteur de 63/64. Ainsi, lorsque l'utilisation de l'espace de bloc varie bloc par bloc, la basefee ne se stabilise que lorsque l'utilisation est légèrement supérieure à t ; en pratique, apparemment d'environ 3 % plus élevée, bien que le nombre exact dépende de la variance.

Proto-danksharding utilise plutôt une formule basée sur un ajustement exponentiel :

bn+1=bn * exp⁡(u−t/8t)

exp⁡(x) est la fonction exponentielle ex où e≈2,71828. Pour de petites valeurs de x, exp⁡(x)≈1+x. En fait, les graphiques pour l'ajustement proto-danksharding et l'ajustement EIP-1559 se ressemblent presque exactement :

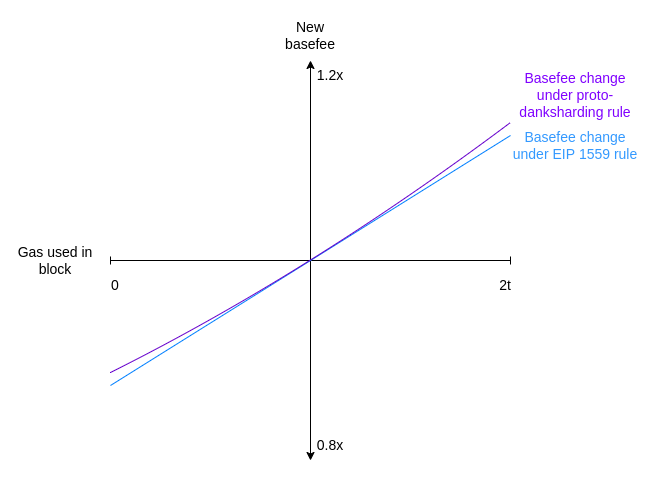
Cependant, la formule exponentielle a l'avantage pratique d'être indépendante du déplacement des transactions : une utilisation totale identique a le même effet sur la basefee, peu importe comment elle est répartie entre différents blocs. En reprenant l'exemple ci-dessus, on peut voir que la formule exponentielle corrige effectivement le problème.

Numéro de bloc	Gaz dans le bloc	Basefee	Basefee utilisant le proto-danksharding
k	-	x	x
k+1	0	⅞ * x	environ 0.88249 * x
k+2	2t	⅞ * 9/8 * x = 63/64 * x	environ 0.88249 * 1.113314 * x = x

Nous pouvons comprendre pourquoi cela est vrai dans le cas général comme suit. La nouvelle basefee bn après un ajustement en plusieurs étapes peut être calculée comme suit :

bn×exp⁡(u1−t8t)×...×exp⁡(un−t8t)

Mais nous pouvons reformuler cette formule différemment :

bn×exp⁡(u1−t8t+...+un−t8t)

=bn×exp⁡(u1+...+un−nt8t)

Et à partir de là, on peut voir que bn dépend uniquement de l'utilisation totale u1+...+un, et non de la répartition de cette utilisation.

Le terme u1+...+un−nt peut être considéré comme l'excès : la différence entre le gaz total réellement utilisé et le gaz total destiné à être utilisé. Le fait que la basefee actuelle soit égale à b0×exp⁡(exceˋs8t) montre clairement que l'excès ne peut pas sortir d'une plage très étroite : si l'excès dépasse 8t×60, alors la basefee devient e60, ce qui est tellement élevé que personne ne peut le payer, et s'il descend en dessous de 0, la ressource est pratiquement gratuite et la chaîne sera spamée jusqu'à ce que l'excès remonte au-dessus de zéro.

Le mécanisme d'ajustement dans proto-danksharding fonctionne exactement en ces termes : il suit actual_total (u1+...+un) et calcule targeted_total (nt), et calcule le prix comme une exponentielle de la différence. Pour simplifier le calcul, au lieu d'utiliser ex, nous utilisons 2x ; en fait, nous utilisons une approximation de 2x : la fonction fake_exponential dans l'EIP. La fausse exponentielle est presque toujours à moins de 0,3 % de la valeur réelle.

Pour éviter que de longues périodes de sous-utilisation ne conduisent à de longues périodes de blocs complets à 2x, nous ajoutons une fonctionnalité supplémentaire : nous n'autorisons pas l'excès à descendre en dessous de zéro. Si actual_total descend jamais en dessous de targeted_total, nous définissons simplement actual_total pour qu'il soit égal à targeted_total à la place. Cela rompt l'invariance de l'ordre des transactions dans des cas extrêmes (où le gaz du blob descend tout le chemin jusqu'à zéro), mais c'est un compromis acceptable pour une sécurité accrue.

Notez également une conséquence intéressante de ce marché multidimensionnel : lors de l'introduction initiale de proto-danksharding, il est probable qu'il aura peu d'utilisateurs au début, et donc pendant un certain temps, le coût d'un blob sera presque certainement extrêmement bas, même si l'activité « régulière » de la blockchain Ethereum reste coûteuse.

L'auteur est d'avis que ce mécanisme d'ajustement des frais est meilleur que l'approche actuelle, et donc éventuellement toutes les parties du marché des frais EIP-1559 devraient passer à son utilisation.

Pour une explication plus longue et plus détaillée, consultez l'article de Dankrad.

Voici le code de fake_exponential pour plus de commodité :

def fake_exponential(numerator: int, denominator: int) -> int:

cofactor = 2 ** (numerator // denominator)

fractional = numerator % denominator

return cofactor + (

fractional * cofactor * 2 +

(fractional ** 2 * cofactor) // denominator

) // (denominator * 3)

Voici le mécanisme central réexprimé mathématiquement, avec l'arrondi supprimé :

FakeExp(x)=2⌊x⌋⋅Q(x−⌊x⌋)

Q(x)=1+23x+13x2

L'objectif est de concaténer de nombreuses instances de Q(x), chacune décalée et mise à l'échelle de manière appropriée pour chaque plage [2k,2k+1]. Q(x) lui-même est une approximation de 2x pour 0≤x≤10≤x≤1, choisie pour les propriétés suivantes :

Simplicité (c'est une équation quadratique)
Correction sur le bord gauche (Q(0)=20=1)
Correction sur le bord droit (Q(1)=2^1=2)
Pente douce (nous nous assurons que Q′(1)=2⋅Q′(0), de sorte que chaque copie décalée et mise à l'échelle de Q a la même pente sur son bord droit que la copie suivante sur son bord gauche)

Les trois dernières exigences fournissent trois équations linéaires à trois coefficients inconnus, et la fonction Q(x) donnée ci-dessus fournit la seule solution.

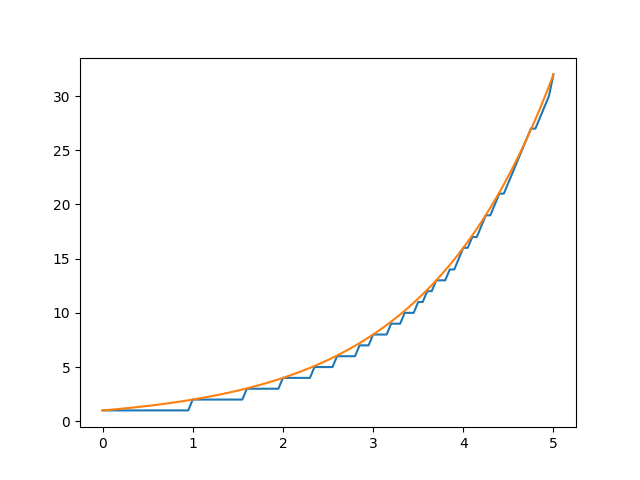
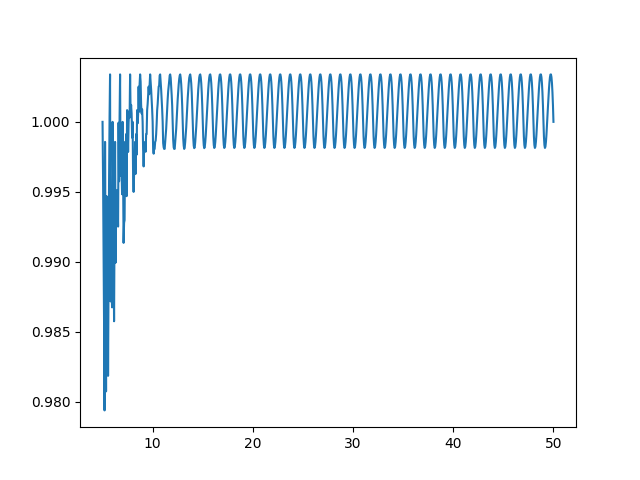
L'approximation fonctionne étonnamment bien ; pour tous sauf les plus petits inputs, fake_exponential donne des réponses à moins de 0.3% de la valeur réelle de 2x :

Image 1. fake_exponential (en bleu) vs actual_value de 2x pour 0≤x≤5, en utilisant un step de 20
Image 2. fake_exponential divisé par actual_value de 2x pour 5≤x≤50,en utilisant un step de 20.

FAQ sur le Proto-Danksharding

Qu'est-ce que le Danksharding ?

Qu'est-ce que le proto-danksharding (aka EIP-4844) ?

Pourquoi est-il acceptable d'ajouter 1 Mo de données à des blocs que tout le monde doit télécharger, mais pas de simplement rendre le calldata 10 fois moins cher ?

Comment le proto-danksharding (EIP-4844) se compare-t-il à l'EIP-4488 ?

Quelles parties du danksharding complet le proto-danksharding implémente-t-il, et que reste-t-il à implémenter ?

Qu'en est-il des exigences d'espace disque qui explosent avec tous ces blocs vraiment gros ?

Si les données sont supprimées après 30 jours, comment les utilisateurs pourraient-ils accéder aux blobs plus anciens ?

Sous quel format se trouve la donnée blob et comment est-elle engagée ?

Pourquoi utiliser le hash du KZG plutôt que le KZG directement ?

Quels sont les deux précompilés introduits dans le proto-danksharding ?

Comment les rollups ZK fonctionnent-ils exactement avec l'engagement KZG de manière efficace ?

Approche facile (nécessite que le rollup utilise le modulo BLS12-381)

Approche modérée : fonctionne avec n'importe quel ZK-SNARK

À quoi ressemble la configuration de confiance KZG ?

À quoi ressemble la configuration de confiance KZG ?

À quel point le KZG est-il "complexe" et "nouveau" ?

Quelles sont les différentes parties logicielles d'une implémentation proto-danksharding ?

À quoi ressemble le marché multidimensionnel des frais du proto-danksharding ?

Comment fonctionne le mécanisme d'ajustement exponentiel des frais de blob EIP-1559 ?

Comment fonctionne fake_exponential ?

Retour en haut

Articles similaires

Articles similaires

Trois étapes pour adhérer à Ethereum France

Retour sur l'Assemblée Générale 2024

Echos de l’Histoire : De l’importance de l’identité décentralisée

Rejoindre discord

Une Question ?