Comprendre la blockchain Ethereum – Article 1 : Bitcoin, première implémentation de la blockchain (2/2)

Deuxième partie de l’article. Pour lire la première partie, c’est ici.

III. Ordonner chronologiquement les transactions à l’échelle du réseau : la blockchain

Nous avons vu comment les transactions sont validées individuellement au niveau de chaque noeud. Il est temps désormais de passer au niveau supérieur, et de voir comment le réseau s’organise dans son ensemble.

III.1. Modèle sans consensus

Un des principaux challenges d’un système décentralisé est de parvenir à un consensus. Ce challenge est particulièrement compliqué lorsque les noeuds de ce système sont anonymes, atomisés et pas nécessairement bien intentionnés. Jusqu’ici, nous avons vu que le registre des comptes était entretenu par des noeuds qui en possèdent chacun une copie. Cependant, pour que l’on sache exactement qui possède quoi, il faut que le réseau s’accorde sur une version du registre. Afin de mieux comprendre, considérons l’exemple suivant, où le réseau n’aurait pas de moyen de s’accorder.

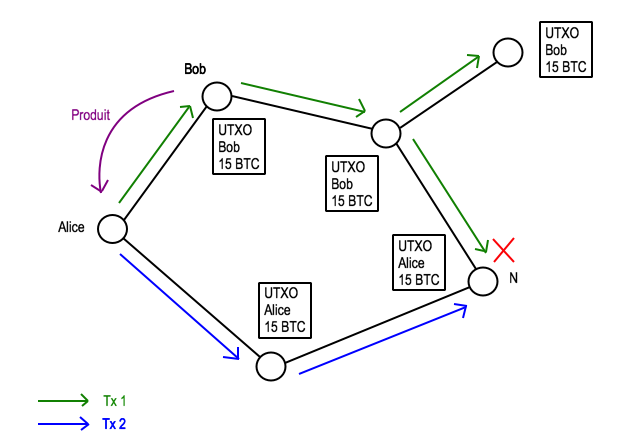
Alice souhaite attaquer le réseau en dépensant deux fois la même somme d’argent (double-spend attack). Nous supposons qu’aucun noeud ne modifie malicieusement le registre. Ainsi, chaque noeud met à jour sa version du registre à chaque fois qu’il reçoit une transaction valide.
Alice crée une première transaction (Tx 1) à destination de Bob, d’un montant de 15 BTC, en échange de quoi Bob lui envoie un objet. Une fois l’objet reçu, elle crée une seconde transaction (Tx 2) à destination d’elle-même et référence en entrée les même UTXOs que pour la transaction précédente.

Ici, du fait de la différence de temps de propagation, le noeud N reçoit la transaction 1 après la transaction 2. N a déjà mis à jour sa base de données des UTXOs, il considère donc la transaction 1 comme invalide, car elle utilise en entrée un UTXO qui n’est plus dans sa base. De manière générale, le réseau n’est pas d’accord sur qui possède les 15 BTC. On peut penser qu’il suffirait d’ajouter la date d’initiation à la transaction, mais il faut se rappeler que le système est décentralisé, et que les noeuds ne doivent à priori pas se faire confiance. En effet, il serait très simple de manipuler cette date pour tromper le réseau. Ce n’est donc pas une solution viable.

III.2. Les bases de la Blockchain

Pour pallier ce problème, Bitcoin propose d’enregistrer de manière ordonnée et horodatée les transactions dans une chaîne de blocs avec laquelle chaque noeud se synchronise : c’est la blockchain. Toutes les 10 minutes, un nouveau bloc de transactions est ajouté à la chaîne. On considère que toutes les transactions d’un même bloc ont eu lieu au même moment.
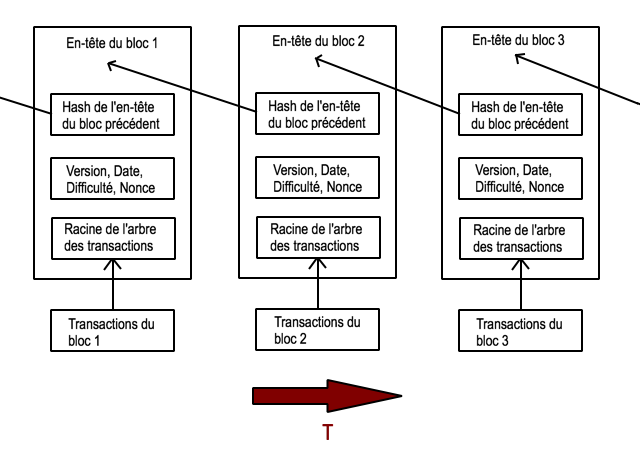
Chaque bloc est constitué de deux parties : une liste de transactions, c’est son contenu, et un en-tête, qui décrit certaines informations relatives au bloc (plus de détails dans la partie Preuve de travail).

L’ajout de bloc s’effectue au niveau de chaque noeud. Ainsi, tous les noeuds possèdent une copie de la blockchain identique (à quelques subtilités près). Chaque bloc référence le bloc précédent, ce qui forme une chaine de bloc, qui s’étend jusqu’au genesis bloc, le tout premier bloc jamais créé.

Il est important de ne pas confondre la chaine de bloc et la chaine de transaction que nous avons évoquée dans l’article précédent. Chaque transaction contenue dans un bloc référence en entrée une ou plusieurs transactions ayant été incluses dans des blocs précédents, formant une chaîne de transaction dont les branches sont multiples. Les blocs sont quant à eux reliés les uns aux autres, chacun pointant vers le bloc précédent, ce qui forme une chaine de bloc qui, sur le long terme, est constituée d’une branche unique.

Le problème présenté dans l’exemple du modèle sans consensus est donc (en partie) résolu. Il suffit que Bob attende que la transaction soit incluse dans un bloc avant d’envoyer le produit. La blockchain étant identique pour chaque noeud, il n’y aura pas de désaccord, l’argent est bien à lui !
Sauf que… pas tout à fait. Certaines attaques sont encore possible. Pour comprendre lesquelles, il convient de s’intéresser au mécanisme de création d’un nouveau bloc.

III.3. Preuve de travail (PoW)

Lorsqu’un noeud reçoit une nouvelle transaction, il la place dans ce qu’on appelle « l’ensemble des transactions non confirmées ». Cet ensemble est propre à chaque noeud, et peut différer d’un noeud à l’autre, du fait du temps de propagation des transactions sur le réseau. C’est une sorte de liste d’attente pour transactions, qui en sortent une fois qu’elles sont incluses dans un bloc.
N’importe quel noeud peut collecter un certain nombre de transactions dans sa liste, vérifier leur validité et former un bloc. Cependant, le bloc n’est pas valide tant que la « preuve de travail » (de l’anglais Proof of Work ou PoW) associée au bloc n’est pas valide. Cela permet entre autres au réseau de ne pas avoir à choisir entre des milliers de blocs possibles mais de s’accorder sur un seul candidat (i.e. sur un set de transactions valides).
Attention, il faut bien faire la différence entre set de transactions valide et bloc valide. Un set de transactions est valide si l’ensemble de ses transactions est valide (pour rappel, un set de transactions constitue le contenu d’un bloc). Un bloc est quant à lui valide si son set de transactions est valide ET si la preuve de travail associée à ce bloc est valide (+ 2 autres conditions, cf. algorithme de validation de bloc plus bas). La preuve de travail n’est pas une preuve de validité du set de transactions, mais une preuve que le mineur a résolu le problème mathématique de non-dépassement de seuil correspondant au bloc (expliqué ci-après).

Il est essentiel de bien comprendre ce qu’est la preuve de travail, car c’est l’un des mécanismes de sécurité fondamentaux du réseau.
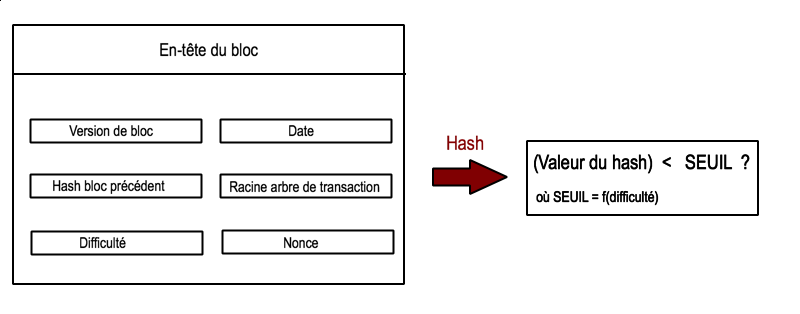
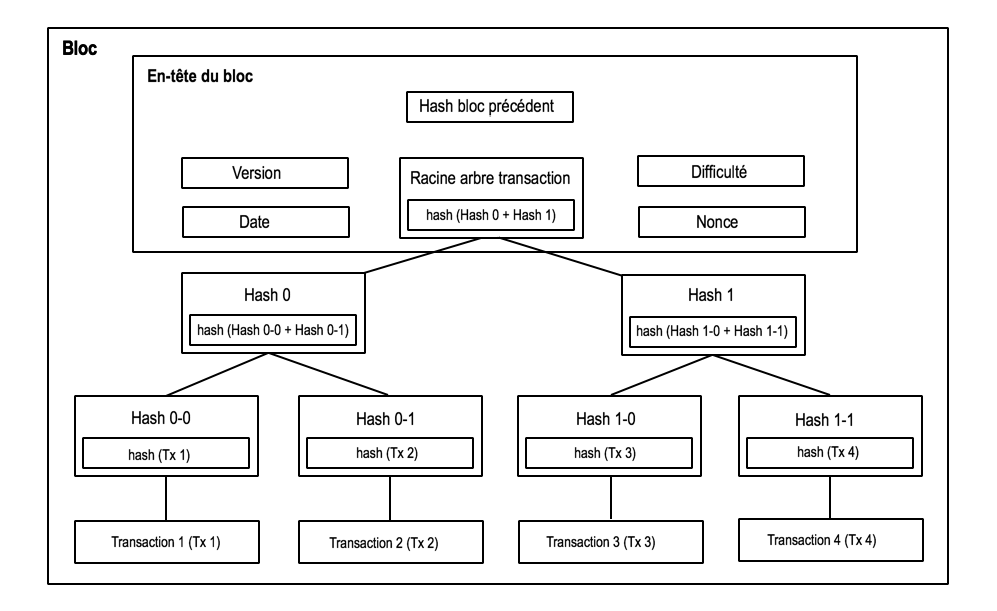
Une fois que les transactions non confirmées sont validées et incluses dans le bloc en préparation, le noeud calcule l’en-tête du bloc. Cet en-tête contient 6 éléments : la version du bloc (définit son type et les règles qu’il suit), l’empreinte (que nous appellerons hash) du bloc précédent, la racine de l’arbre de transactions (plus de précisions plus bas), la date, la difficulté et un nonce.

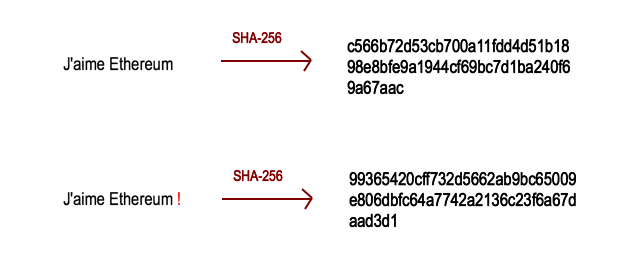
À ce stade, il nous faut expliquer ce qu’est une fonction de hachage. Une fonction de hachage est une fonction à sens unique qui produit un hash à partir d’un message donné. Comme pour les fonctions vues dans la partie clé privée/clé publique, il n’est pas possible de retrouver le message à partir du hash, et tout changement même infime dans le message implique un important changement du hash (NB : On parle ici de message, mais on peut très bien produire un hash à partir d’un fichier. Après tout, un fichier n’est qu’un gros message informatique).
Bitcoin utilise la fonction de hachage SHA-256, qui produit un hash de 256 bits de longueur (voir ci-dessous).

Voyez à quel point le hash change après simple ajout d’un point d’exclamation !

Revenons à notre en-tête. Pour le moment, nous ne nous attarderons pas sur les 4 premiers éléments (nous supposons qu’ils sont facilement identifiables). Restent la difficulté et le nonce. C’est sur ces deux éléments que va s’effectuer la preuve de travail.

L’idée est la suivante : le hash de l’en-tête du bloc doit, pour que la preuve de travail soit valide, être inférieur à un certain nombre que l’on nomme seuil et qui est défini par la difficulté. Comme les 4 premières informations changent à chaque bloc et qu’il est impossible de prédire la valeur du hash sans appliquer la fonction SHA-256, la seule manière d’obtenir un hash valide est de tester différents nonce jusqu’à obtenir un hash correspondant au niveau de difficulté.

En regardant la forme d’un hash, il est légitime de se demander comment on peut comparer un tel message avec un nombre. En réalité, le hash est un nombre hexadécimal, ce qui signifie que les chiffres qui le composent sont dans l’ensemble {0,1,2,3,4,5,6,7,8,9,a,b,c,d,e,f}, où (a,b,c,d,e,f) correspond à (10,11,12,13,14,15). Pour convertir le hash en base décimale (celle que nous utilisons tous les jours), il faut multiplier chaque chiffre par 16ⁱ, i étant la position du chiffre dans le hash, en partant de la droite et à partir de 0.

Exemple : 2ba5 = 2*16³ + 11*16² + 10*16¹ + 5*16⁰ = 8192 + 2816 + 160 + 5 = 11 173.

Un hash est composé de 64 chiffres, sa valeur est donc majorée par 16⁶⁴. Le seuil fixe une limite inférieure à 16⁶⁴, afin que la recherche de hash ne soit pas triviale (en d’autres termes, qu’elle demande un effort de calcul à l’ordinateur).
Par exemple, si on place un seuil à 16⁵⁸, l’ordinateur devra calculer des hash en incrémentant le nonce à chaque échec, jusqu’à en trouver un inférieur à 16⁵⁸, ou qui commence par 000000 (64-58=6 zéros), ce qui revient au même. En effet, un hash de la forme 000000xxx….xxxx sera forcément inférieure à 16⁵⁸, puisque toute somme de termes de la forme x*16ⁱ où i<58 et x<16 ne peut jamais dépasser 16⁵⁸.

On comprend ici que plus le seuil est bas, plus le nombre de 0 requis en début de hash est important, et donc plus il est difficile de trouver un nonce valide.

En paradigme, la preuve de travail peut être exprimée comme suit :

Tant que (valeur du hash) ≥ seuil :

1.  Calculer le hash de l’en-tête du bloc
2.  Si (valeur du hash) < seuil, retourner le hash
Sinon, incrémenter le nonce de 1 (=ajouter 1 au nonce)

Pour un noeud seul, il faudrait en moyenne plusieurs années pour trouver un bloc valide. À l’échelle du réseau, la difficulté est établie de telle sorte qu’il faut en moyenne 10 minutes pour qu’un noeud trouve un bloc valide. Le noeud « gagnant » ajoute son bloc à la chaîne, on dit qu’il a « miné le bloc ». Il reçoit en compensation une somme fixe déterminée par le réseau (25 BTC aujourd’hui) ainsi que les éventuels frais de transaction (voir partie 1 pour la définition de frais de transaction).
Bitcoin encourage donc les mineurs à entretenir le réseau en les récompensant par une rémunération. C’est par ailleurs de cette manière que les bitcoin sont introduits dans l’écosystème (une chaîne de transactions commence toujours par un UTXO attribué à un mineur).

La preuve de travail a une autre implication d’importance : plus un mineur possède une capacité de calcul élevée, plus la probabilité qu’il trouve le prochain bloc est élevée. C’est pourquoi on a vu se former des « pool », ou coopératives, de mineurs qui mettent en commun leurs capacité de calcul afin de régulariser leur revenus.
La puissance de calcul d’un mineur par rapport à l’ensemble du réseau permet d’estimer ses chances de gagner seul la course au nonce qui produira le hash valide. En pratique, elles sont extrêmement faibles. En revanche, dans une coopérative, la mise en commun de la puissance de calcul permet de trouver des nonces valides plus régulièrement et d’assurer de fait des revenus plus stables aux mineurs qui y participent.

À noter également : plus il y a d’ordinateurs dans le réseau, plus le temps moyen pour trouver un bloc est faible. Pour conserver un temps moyen de bloc à 10 minutes, le réseau ajuste la difficulté tous les 2016 blocs. Le pourquoi de ces 10 minutes sera discuté dans un prochain article.

Dès qu’un mineur a trouvé un bloc valide, il le transmet au réseau. Chaque noeud qui reçoit ce bloc vérifie sa validité grâce à l’algorithme suivant :

1.  Vérifier que le bloc précédent existe et est valide (revient à vérifier que le hash du  dernier bloc correspond bien à l’élément « hash du bloc précédent » référencé en en-tête du bloc en cours de vérification)
2.  Vérifier que la date du bloc est supérieure à la date du bloc précédent et inférieure à 2h après
3.  Vérifier que la preuve de travail est valide (i.e. le hash de l’en-tête du bloc est inférieur au seuil)
4.  Vérifier l’ensemble des transactions. Si l’une d’entre elles retourne une erreur, stopper et retourner FAUX
5.  Mettre à jour l’ensemble des transactions non vérifiées et retourner VRAI

Si l’algorithme retourne vrai, le bloc est considéré valide et le noeud l’ajoute à la blockchain. Dans le cas où ce noeud est un mineur, il se met alors à la recherche du prochain bloc : il collecte un nouveau set de transactions dans l’ensemble des transactions non vérifiées et recommence la preuve de travail pour ce set.

III.4. Temps de latence

Une considération technique à prendre en compte est le temps de latence. Le temps de latence, ou temps de propagation, est le délai entre le moment auquel un bloc valide est émis par un mineur et celui où il est reçu par un noeud. En moyenne, il est de 12.6 secondes. Ce délai explique pourquoi, en fin de chaîne, les noeuds peuvent pendant un certain temps ne pas avoir la même copie de la blockchain (ce sont les subtilités dont nous avions parlé plus haut). En effet, tant que le bloc valide ne s’est pas propagé jusqu’à un mineur donné, celui-ci continue de chercher le prochain bloc. En moyenne, un bloc concurrent valide (pouvant contenir un set différent de transactions valides) peut donc être trouvé pendant 12.6 secondes après que le premier bloc valide ait été trouvé. Dans ce cas, deux blocs valides circulent sur le réseau. Chaque mineur cherche le prochain bloc à partir du premier bloc qu’il reçoit.

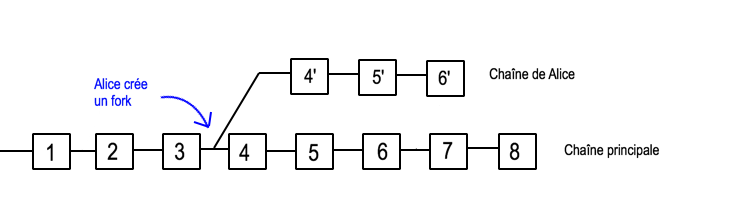
En pratique, un mineur recevant un bloc concurrent (donc ayant déjà reçu un bloc valide) ne le rejette pas. Il crée un « fork » (voir schéma ci-après) et mine sur la chaîne du premier bloc qu’il a reçu (i.e. l’élément « hash de l’en-tête du bloc précédent » du bloc qu’il tente de créer a pour valeur celui du premier bloc valide reçu). Si il reçoit un nouveau bloc valide, il passera sur la chaîne dont le dernier bloc est celui à partir duquel le nouveau bloc valide a été miné. C’est une règle fondamentale de la blockchain : la chaîne la plus longue l’emporte toujours.

Ainsi, la chaîne retrouve son unicité dès qu’un nouveau bloc (N) est créé, à moins qu’un mineur travaillant sur la chaîne la plus courte trouve un nouveau bloc concurrent dans le temps de latence suivant l’émission du bloc (N).
Dans certains cas extrêmes, des fork peuvent subsister sur de nombreux blocs, mais la règle de la chaîne la plus longue permet d’aboutir à une stabilisation de la chaine au bout d’un certain temps.

III.5. Nouvelle règle, nouveaux problèmes

Vous souvenez-vous des attaques que nous avions évoqué avant d’aborder la preuve de travail ? Il est temps de les expliquer. La règle de la chaîne la plus longue est bien pratique pour stabiliser la chaîne de blocs et garantir son unicité, mais elle ouvre aussi la porte à une nouvelle forme de double-spend attack.

Reprenons l’exemple de Alice et Bob. Alice envoie 15 BTC à Bob en échange d’un produit. Bob attend que la transaction soit incluse dans la blockchain, puis envoie le produit. Alice crée alors un fork dans la chaîne en amont du bloc dans lequel la transaction à destination de Bob a été incluse, et remplace cette dernière par une autre transaction où elle s’envoie la somme à elle-même. Si Alice parvient à proposer une chaîne plus longue que la chaîne principale, alors tout le réseau adoptera la nouvelle chaîne proposée par Alice, et Bob perdra ses 15 BTC.

Bien que théoriquement possible, cette attaque est en réalité très difficile à mener. En effet, pendant que Alice travaille sur sa chaîne, l’ensemble du réseau travaille sur la chaîne principale. Alice, au même titre que l’ensemble des noeuds du réseau, n’a aucun moyen de calculer facilement le prochain bloc (rappelons que dans la preuve de travail le « hash de l’en-tête du bloc précédent » est un des paramètres d’entrée).
Pour qu’elle soit certaine de gagner la « course » à la chaîne la plus longue, il faudrait qu’elle possède une capacité de calcul supérieure à celle du reste du réseau. En d’autres termes, il faudrait qu’elle possède au moins 51% de la capacité totale de calcul du réseau : c’est pourquoi on appelle ce type d’attaque une « attaque 51% ».
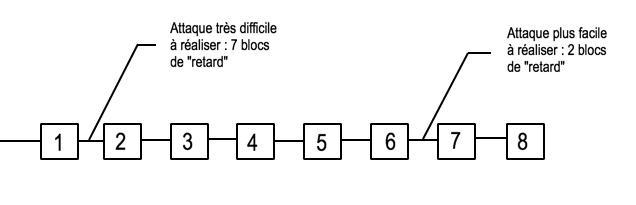
Cette attaque explique pourquoi la fin de chaîne est considérée comme moins sécurisée. En effet, plus on part avec un « retard » de blocs important par rapport à la chaîne principale et plus il est compliqué de proposer une chaine plus longue (la difficulté de l’attaque augmente exponentiellement à mesure que l’on recule dans la chaine). On pourrait penser qu’un attaquant puisse décider de laisser son ordinateur tourner pour tenter de rattraper la chaine principale. Même si la probabilité est très faible, en attendant suffisamment longtemps, il pourrait peut-être finir par gagner. Cependant, cette stratégie n’est pas viable économiquement. Le temps moyen pour rattraper la chaine principale en partant avec un retard considérable est si important que la facture d’électricité associée serait colossale. Pour réduire ce temps, il faudrait posséder plus d’ordinateurs, et donc payer plus d’électricité. Une attaque est donc dans tous les cas très coûteuse à réaliser, et ce coût augmente avec le retard par rapport à la chaine principale.

De manière générale, il est conseillé, par mesure de précaution, d’attendre plusieurs blocs avant de considérer une transaction finalisée. En effet, certaines coopératives ont atteint des capacités de calcul très élevées, et pourraient potentiellement mener une attaque à bien. Une coopérative n’a en théorie pas besoin de posséder plus de la moitié de la capacité de calcul du réseau pour mener une attaque à bien. Plus elle a de capacité de calcul, plus ses chances de réussites sont élevées (simplement, la coopérative est certaine de réussir en un temps fini si elle possède plus de 50% de la capacité de calcul du réseau).

Rassurez-vous cependant, les coopératives n’ont de manière rationnelle que peu d’intérêt à effectuer ce genre attaque. En effet, lors d’une attaque, une coopérative peut uniquement inverser une transaction qu’elle a effectuée, elle n’est pas en mesure d’inverser la transaction d’une autre personne, de créer des Bitcoin ou d’envoyer des Bitcoin qui ne lui appartiennent pas. Il en résulte que le bénéfice potentiel est en moyenne négatif tant qu’elle possède moins de 50% de la capacité de calcul du réseau.
De plus, une coopérative n’est pas une entité guidée par une volonté unique, mais est un ensemble constitué d’une multitude de mineurs individuels. Le gérant de la coopérative peut décider de ne pas être honnête, mais, dans ce cas, rien n’empêche les mineurs de quitter la coopérative pour en rejoindre une honnête. Tant que les mineurs constituant une coopérative seront attentifs à la politique de cette dernière (et honnêtes), le risque est minime.

NB : Un article détaillé sur les coopératives, les probabilités de succès d’une double-spend attack et la centralisation du réseau sera disponible prochainement.

III.6. Des noeuds et des arbres

Comme indiqué dans le schéma « Fonctionnement simplifié de la Blockchain », l’en-tête d’un bloc contient la racine de l’arbre des transactions.
Chaque bloc contient une liste de transactions organisée dans un arbre de Merkle. Un arbre de Merkle est un arbre binaire dont les feuilles (c’est à dire les éléments de plus bas niveau) sont les transactions, et dont les noeuds intermédiaires sont soit des hash de somme de noeuds intermédiaires, soit des hash de transactions. Le noeud de plus haut niveau est appelé racine, c’est lui qui est inclus dans l’en-tête du bloc.
Attention à ne pas confondre noeud du réseau et noeud d’arbre de Merkle. Le terme noeud dans un arbre binaire désigne les éléments de cet arbre.

L’arbre de Merkle est essentiel à la scalabilité du réseau, c’est à dire à sa capacité à monter en charge. Pour en comprendre la raison, il nous faut d’abord revenir sur la notion de noeud sur le réseau et leur typologie.

Jusqu’à maintenant, nous avons considéré que tout ordinateur connecté au réseau était un noeud vérifiant l’intégralité de la blockchain. En réalité, ce n’est pas tout à fait le cas. Grossièrement, on distingue 3 types de noeuds : les noeuds complets (« full node »), les mineurs et les noeuds légers (« lightweight-node »).
Les premiers sont les noeuds auxquels je vous ai habitués depuis le début de l’article. Ce sont des noeuds vérificateurs : à chaque bloc reçu, ils vérifient l’ensemble des transactions, ainsi que la preuve de travail. Lors de sa première connexion au réseau, un noeud complet télécharge donc l’historique complet de la blockchain, et vérifie au passage toutes les transactions.
Les mineurs quant à eux sont des noeuds complets qui consacrent une partie de leur capacité de calcul à la preuve de travail : ce sont eux qui produisent les blocs.
NB : Si le mineur fait partie d’une coopérative, il ne se connecte pas forcément en tant que noeud complet. La coopérative utilise un nombre de noeuds complets en général inférieur au nombre de mineurs qui la composent.

Les noeuds complets sont indispensables au réseau, mais ils sont également très contraignants à l’usage.
Aujourd’hui, un noeud complet requiert environ 80 Go d’espace disque et 2 Go de RAM. Beaucoup d’utilisateurs n’ont pas autant d’espace, et il est impensable d’envisager l’installation d’un noeud complet sur mobile ! De plus, un noeud complet vérifie l’ensemble des transactions à chaque nouveau bloc, ce qui demande beaucoup de ressources.
À l’inverse, un client léger ne télécharge que les en-têtes des blocs (+ éventuellement quelques transactions qui l’intéressent), ce qui permet de garantir la validité de la preuve de travail et l’intégrité de la chaine de transactions tout en économisant beaucoup d’espace mémoire. En effet, un arbre de Merkle est structuré de telle sorte que tout changement au niveau d’une des feuilles se répercute de noeud en noeud jusqu’à la racine. Par conséquent, si un noeud complet malicieux tentait de remplacer une transaction par une autre dans un bloc donné, un client léger serait capable de repérer la fraude en constatant que le « hash du bloc précédent » du bloc suivant n’a plus la même valeur.

Un client léger doit néanmoins être capable de vérifier la validité des transactions qui le concernent. N’ayant pas de base des UTXOs, il ne peut pas faire une vérification formelle comme celle que nous avons vu dans la partie 1. À la place, il utilise la profondeur du bloc comme garantie de validité. Pour savoir si une transaction lui étant adressée a été incluse dans un bloc, le client léger envoie ce que l’on appelle un filtre de Bloom au réseau. Ce dernier indique que si une transaction est envoyée à une des adresses ayant de l’intérêt pour le client, alors la branche de l’arbre de Merkle correspondante sera téléchargée en plus du header du bloc. Ainsi, le client léger sait dans quels blocs sont incluses les transactions qu’il reçoit. Ensuite, il attend qu’un nombre X de blocs (appelés confirmations) soient ajoutés à la chaîne. Ces X blocs garantissent que suffisamment de travail a été effectué depuis l’ajout de la transaction. Si, par exemple, X=39, le client considèrera une transaction reçue comme valide une fois que 39 blocs auront été ajoutés à la suite de celui qui la contient.

Si les noeuds légers sont très utiles, ils n’en restent pas moins à double tranchant. L’une des principales forces du réseau Bitcoin est la faible dose de confiance requise entre les utilisateurs. Le seul moyen d’être assuré de la validité des transactions est d’utiliser un client noeud complet.
Pour vous en convaincre, considérez un réseau où la plupart des noeuds seraient des noeuds légers. Dans ce cas, il suffirait de corrompre les quelques noeuds complets du réseau pour pouvoir le manipuler, car personne d’autre qu’eux ne valide les transactions.
Il est donc conseillé d’utiliser un client noeud complet pour pouvoir profiter pleinement de l’aspect décentralisé du réseau.

En pratique, le client que vous utilisez pour vous connecter définit votre type de noeud.
Sur Ethereum, Mist est un client noeud complet. Bitcoin propose des SPV-clients (comme Multibit), qui permettent de se connecter en tant que noeud léger. La politique de ces clients est de faire confiance à la majorité des mineurs.
Enfin, la plupart des webwallets ne vous connectent même pas au réseau, ce sont eux qui s’y connectent à votre place. Ce sont donc des services centralisés, dans lesquels vous prenez le risque de placer votre confiance. À bon entendeur !

Ainsi se conclut la partie Bitcoin de la série. Nous allons désormais pouvoir nous attaquer au plat de résistance : Ethereum !

Suite à paraître prochainement