Traduction française intégrale du document Sharding FAQ rédigé par Vitalik Buterin, dans sa version au 7 juillet 2017 ; réalisée par Jean Zundel pour l’Asseth et Ethereum France.
Introduction
Aujourd’hui, tous les protocoles de blockchains dépendent d’un modèle où tous les nœuds stockent tous les états (soldes de comptes, code et stockage de contrat, etc.) et traitent toutes les transactions. Cela fournit une sécurité importante mais limite énormément le passage à l’échelle, ou scaling, des blockchains : une blockchain ne peut pas traiter plus de transactions qu’un seul nœud du réseau. C’est en grande partie à cause de cela que Bitcoin est limité à ~3-7 transactions par seconde, Ethereum à 7-15, etc. Cependant, cela pose une question : y a-t-il de moyen créer un nouveau mécanisme qui se démarquerait du modèle où littéralement chaque ordinateur du réseau vérifie littéralement chaque transaction, et qui ne requerrait que de petits sous-ensembles de nœuds pour vérifier chaque transaction ? Tant qu’il existe suffisamment de nœuds pour vérifier les transactions de manière extrêmement sûre, mais suffisamment peu pour que le système puisse traiter de nombreux groupes de transactions en parallèle, ne pouvons-nous pas utiliser cette technique pour augmenter considérablement le débit de la chaîne ?
Quelles sont les manières triviales mais défectueuses de résoudre ce problème ?
Il y a trois catégories de solutions simples. La première consiste à abandonner le passage à l’échelle de chaque blockchain et de supposer que les utilisateurs vont employer plusieurs « altcoins ». Cela augmente de beaucoup le débit mais au prix de la sécurité : une multiplication par N du débit par cette méthode implique nécessairement une division par N de la sécurité. Elle n’est donc pas viable pour de grandes valeurs de N.
La deuxième repose simplement sur la limitation de la taille des blocs. Cela peut fonctionner jusqu’à un certain point, et dans certaines situations peut constituer la solution correcte car la taille des blocs peuvent être plus contraintes par la politique que par des considération strictement techniques mais, indépendamment des croyances des uns et des autres concernant des cas précis, ce type d’approche a des limites inévitables : si on va trop loin, les nœuds tournant sur du matériel générique abandonneront la partie, le réseau commencera à dépendre uniquement d’un très petit nombre de super-ordinateurs faisant tourner la blockchain, et cela peut engendrer un énorme risque de centralisation.
La troisième est le « minage combiné » ou merge mining, une technique où cohabitent de nombreuses chaînes qui partagent toutes la même puissance de minage (ou l’enjeu dans les systèmes à preuve d’enjeu). Actuellement, une grande partie de la sécurité de Namecoin provient de la blockchain de Bitcoin avec cette méthode. Si tous les mineurs participent, cela augmente le débit d’un facteur N sans compromettre la sécurité. Se pose cependant le problème de l’accroissement de la charge de calcul et de stockage sur chaque mineur d’un facteur N, et cette solution n’est donc qu’une forme cachée d’augmentation de la taille des blocs.
Même si l’on considère cette solution acceptable, il reste le défaut que les chaînes ne sont pas vraiment « liées ensembles » ; seul un petit montant d’incitation économique est requis pour convaincre les mineurs d’abandonner ou de compromettre une chaîne donnée. Cette possibilité est en fait très réelle ; historiquement, on a connu de véritables incidents concernant des chaînes en minage combiné, ainsi que des développeurs qui ont explicitement plaidé en faveur des attaques sur le minage combiné en tant que mécanisme de « gouvernance », en détruisant les chaînes n’étant pas « profitables » pour une certaine coalition.
Si seuls quelques mineurs participent au minage combiné de chaque chaîne, le risque de centralisation est atténué mais les avantages en termes de sécurité du minage combiné sont également très réduits.
On dirait qu’il y a une sorte de « trilemme » du passage à l’échelle en jeu. Quel est ce trilemme et peut-on le résoudre ?
Le trilemme dit que les systèmes de blockchain ne peuvent posséder que deux des trois propriétés suivantes :
- Décentralisation (définie comme le systéme étant capable de fonctionner dans un scénario où chaque participant n’a accès qu’à O(c) ressources, c’est-à-dire un ordinateur portable ou un petit serveur virtuel) ;
- Passage à l’échelle (défini comme étant capable de traiter O(n) > O(c) transactions ;
- Sécurité (définie comme étant sûr contre des attaquants disposant de ressource allant jusqu’à O(n).
Dans la suite de ce document, nous continuerons d’employer c pour référer à la quantité de ressources informatique (comme le calcul, la bande passante et le stockage) disponible pour chaque nœud, et n pour nous référer à la taille de l’écosystème dans un sens abstrait ; nous supposons que la charge transactionnelle, la taille de l’état et la capitalisation totale d’une crypto-monnaie sont toutes proportionnelles à n.
Certains prétendent qu’en raison de la loi de Metcalfe, la capitalisation d’une crypto-monnaie devrait être proportionnelle à n^2 et non à n. Est-ce exact ?
Non.
Pourquoi pas ?
La loi de Metcalfe prétend que la valeur d’un réseau est proportionnelle au carré du nombre d’utilisateurs car, si un réseau possède n utilisateurs, le réseau a de la valeur pour chaque utilisateur, mais cette valeur est elle-même proportionnelle au nombre d’utilisateurs parce que si un réseau a n utilisateurs, il y a n-1 connexions potentielles à travers le réseau dont l’utilisateur peut bénéficier.
En pratique, des recherches empiriques suggèrent que la valeur d’un réseau avec n utilisateurs est proche d’une « proportionnalité de n^2 pour de petites valeurs de n et d’une proportionnalité de (n × log n) pour de grandes valeurs de n ». Cela a du sens car, pour les petites valeurs, l’argument est vrai mais, une fois qu’un système grandit, deux effets ralentissent la croissance. D’abord, la croissance se produit souvent en pratique dans des communautés, et dans un réseau de taille moyenne le réseau fournit déjà la plupart des connexions importantes pour tout le monde. Ensuite, les connexions peuvent souvent se substituer à d’autres et on peut arguer de ce que les gens ne dérivent qu’une valeur de ~O(log(k)) de k connexions : il est appréciable d’avoir accès à 23 marques de déodorant mais pas beaucoup plus que pour 22, alors que la différence entre un choix et zéro est très significatif.
De plus, même si la valeur d’une crypto-monnaie est proportionnelle à O(k * log(k)) avec k utilisateurs, si nous acceptons l’explication qui précède pour l’expliquer, alors cela implique aussi que le volume de transaction est également O(k * log(k)), puisque la valeur log(k) par utilisateur provient théoriquement de ce que cet utilisateur effectue log(k) connexions à travers le réseau et la taille de l’état devrait également croître selon O(k * log(k)) dans de nombreux cas puisqu’il existe au moins certains types d’état qui sont spécifiques aux relations au lieu d’être spécifiques aux utilisateurs. Donc, supposer que n = O(k * log(k)) et tout faire reposer sur n (taille de l’écosystème) et c (puissance de calcul d’un seul nœud) est un modèle qui convient parfaitement.
Quelles sont les manières modérément simples mais seulement partielles de résoudre le problème du passage à l’échelle ?
De nombreuses propositions de fragmentation (comme cette ancienne proposition de fragmentation BFT de Loi Luu et al. à la National University of Singapore, ainsi que l’approche de cet arbre Merklix [footnote]Arbre Merklix == Arbre de Merkle Patricia[/footnote] qui a été suggérée pour Bitcoin) tentent de ne fragmenter que le traitement des transactions ou que l’état des fragments, sans toucher au reste[footnote]Les propositions ultérieures du groupe de NUS arrivent effectivement à fragmenter l’état, grâce aux techniques de reçus et de compactage de l’état que je décrirai plus loin dans ce document.[/footnote]. Ces efforts sont admirables et peuvent mener à certains gains en performances mais leur principal problème est qu’ils ne résolvent que l’un des deux goulets d’étranglement. Il faut pouvoir traiter plus de 10000 transactions par seconde sans forcer chaque nœud à être un super-ordinateur, ni à stocker un téraoctet de données d’état, et cela demande une solution complète où la charge de travail résultant du stockage de l’état, du traitement des transactions et même du téléchargement et de la rediffusion des transactions est répartie sur tous les nœuds.
On note en particulier que cela demande des changements au niveau P2P car un modèle de diffusion générale ne passe pas à l’échelle puisqu’il demande à chaque nœud de télécharger et rediffuser O(n) données (chaque transaction envoyée), alors que notre critère de décentralisation suppose que chaque nœud n’a accès qu’à O(c) des ressources de tous types.
Et les approches qui tentent de ne rien « fragmenter » ?
Bitcoin-NG peut améliorer dans une certaine mesure le passage à l’échelle au moyen d’une conception différente de la blockchain qui rend beaucoup plus sûr pour le réseau le fait que les nœuds passent une grande partie de leur temps CPU à vérifier les blocs. Dans les blockchains simples en preuve de travail, les risques de centralisation sont énormes et la sécurité du consensus est affaiblie si la capacité est augmentée jusqu’au point où plus d’environ 5% du temps CPU des nœuds est passé à vérifier des blocs ; la conception de Bitcoin-NG atténue ce problème.
Cependant, le passage à l’échelle n’est amélioré que d’un facteur constant de peut-être 5 à 50[footnote]On a ici quelques raisons d’être conservateur. En particulier, notons que si un attaquant lance des transactions nocives dont le rapport entre le temps de traitement et les dépenses en espace de bloc (octets, gaz, etc.) est beaucoup plus haut que d’habitude, alors le système sera victime de très mauvaises performances et un facteur de sécurité s’avère nécessaire pour prendre en compte cette possibilité. Dans les blockchains traditionnelles, le fait que le traitement des blocs ne prenne que ~1-5% du temps de bloc a pour principal rôle de protéger contre le risque de centralisation mais sert aussi à protéger contre le risque de déni de service. Dans le cas spécifique de Bitcoin, sa pire vulnérabilité actuelle connue d’exécution quadratique limite sans aucun doute tout passage à l’échelle à ~5-10% actuellement, et dans le cas d’Ethereum, bien que toutes les vulnérabilités connues sont ou ont été éliminées après les attaques par déni de service, il reste encore un risque d’anomalies potentielles, en particulier sur une plus petite échelle. Dans Bitcoin NG, le besoin de celui-là n’existe plus mais le besoin de celui-ci reste présent.[/footnote],[footnote]Une autre raison d’être prudent est qu’une plus grande taille d’état correspond à un débit réduit, puisque il sera de plus en plus difficile pour les nœuds déconserver les données d’état en RAM. Ils auront de plus en plus besoin d’accès aux disques et les bases de données, qui ont souvent un temps d’accès de O(log(n)), seront de plus en plus lentes en accès. C’est une leçon importante apprise de la dernière attaque par déni de service sur Ethereum, qui a gonflé l’état de ~10 Go en créant des comptes vides et a donc indirectement ralenti le traitement en forçant les accès à l’état à utiliser le disque au lieu de la RAM.[/footnote] et n’améliore pas le passage à l’échelle de l’état. Cela dit, les approches de style Bitcoin-NG n’excluent pas la fragmentation et les deux peuvent certainement être implémentées en même temps.
Les stratégies à base de channels (Lightning Network, Raiden, etc.) peuvent faire passer à l’échelle la capacité de transaction d’un facteur constant mais ne peuvent rien pour le stockage de l’état, et s’accompagnent de leurs propres compromis et limitations, en particulier en ce qui concerne les attaques par déni de service ; le passage à l’échelle sur la chaîne même par fragmentation (plus d’autres techniques) et le passage à l’échelle hors chaîne par les channels sont indiscutablement nécessaires et complémentaires.
Il existes des approches faisant usage de cryptographie avancée, comme Mimblewimble et d’autres fondées sur les zk-SNARK, pour résoudre une partie spécifique du problème de l’échelle : la synchronisation initiale. Au lieu de vérifier l’intégralité de l’historique depuis la genèse, les nœuds pourraient vérifier une preuve cryptographique selon laquelle l’état actuel découle légitimement de l’historique. Ces approches résolvent un vrai problème, bien qu’on puisse noter qu’on peut employer la crypto-économie au lieu de la pure cryptographie pour résoudre le même problème de manière plus simple – voir l’implémentation actuelle dans Ethereum du fastsyncing et du warp syncing.
Aucune de ces solutions ne peut quoi que ce soit à la croissance de la taille de l’état ou aux limites du traitement des transactions en ligne.
Taille de l’état, historique, crypto-économie, houla ! Définissez certains de ces termes avant d’aller plus loin !
- État (State) : un ensemble d’informations qui représente « l’état courant » d’un système ; la détermination de la validité ou non d’une transaction, ainsi que de ses effets, ne devrait dépendre que de l’état dans le modèle le plus simple. On peut citer comme exemples de données d’état l’ensemble des UTXO dans Bitcoin, les soldes + les nonces + le code + le stockage dans Ethereum et les entrées du registre des noms dans Namecoin.
- Historique (History) : une liste ordonnée de toutes les transactions qui se sont produites depuis la genèse. Dans un modèle simple, l’état présent devrait être une fonction déterministe de l’état de genèse et de l’historique.
- Transaction: un objet qui entre dans l’historique. En pratique, une transaction représente une opération que certains utilisateurs désirent effectuer et qui est signée cryptographiquement.
- Fonction de transition d’état (State transition function) : une fonction qui prend un état, lui applique une transaction et sort un nouvel état. Les calculs que cela implique peuvent comprendre l’ajout et la soustraction de soldes au niveau de comptes spécifiés par la transaction, en vérifiant les signatures numériques et en lançant du code de contrats.
- Arbre de Merkle (Merkle tree) : une structure arborescente d’empreintes cryptographiques qui stockent une très grande quantité de données, où l’authentification de chaque donnée individuelle ne prend que O(log(n)) dans l’espace et le temps. Voir plus de détails ici. Dans Ethereum, l’ensemble des transactions de chaque bloc, ainsi que l’état, est conservé dans un arbre de Merkle et les racines des arbres sont commitées dans un bloc.
- Reçu (Receipt) : un objet représentant l’effet d’une transaction, qui n’est pas stocké dans l’état mais qui reste bien stocké dans un arbre de Merkle afin que son existence puisse être facilement prouvée même par un nœud qui ne dispose pas de toutes les données. Les logs d’Ethereum sont des reçus ; dans les modèles fragmentés, les reçus sont utilisés pour faciliter les communications inter-fragments asynchrones.
- Client léger (Light client) : une manière d’interagir avec une blockchain qui ne requiert qu’une très petite quantité (disons O(1), bien que O(log(c)) puisse être pertinent dans certains cas) de ressources informatiques, en ne conservant que la trace des en-têtes de blocs de la chaîne par défaut et en acquérant toutes les informations nécessaires sur les transactions, l’état ou les reçus en demandant et en vérifiant les preuves de Merkle des données correspondantes au coup par coup.
- Racine d’état (State root) : l’empreinte de l’arbre de Merkle représentant l’état[footnote]Dans les blockchains fragmentées, il n’y a pas nécessairement de consensus synchrone sur un état global unique, et le protocole ne demande donc jamais au nœuds d’essayer de calculer une racine d’état globale ; en fait, dans les protocoles présentés plus loin, chaque fragment possède son propre état et pour chaque fragment il existe un mécanisme d’engagement (commit) sur la racine d’état de ce fragment, qui représente l’état du fragment.[/footnote]
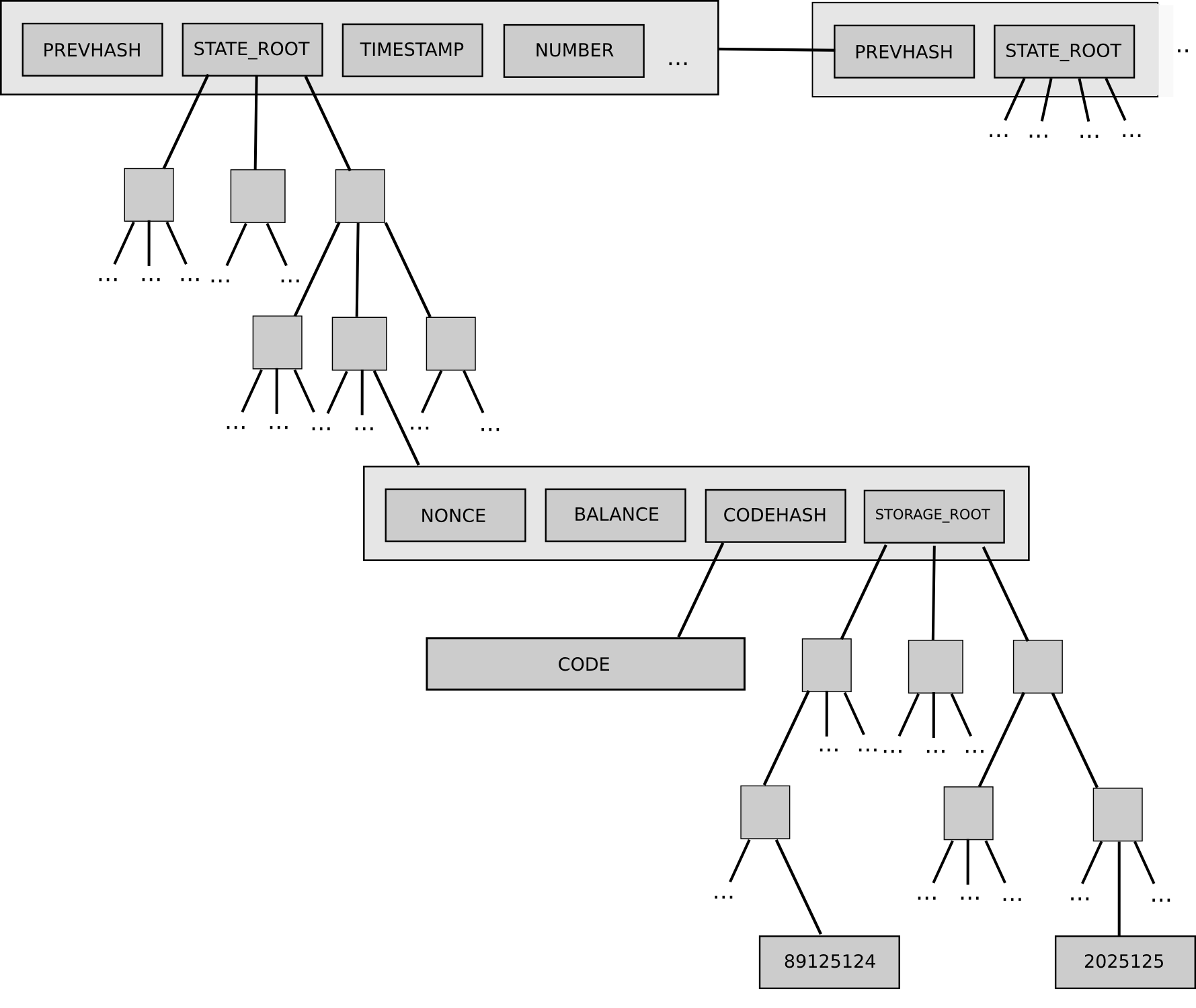
L’arborescence d’état d’Ethereum et la manière dont celle-ci s’insère dans la structure des blocs
Quel est le principe fondamental de la fragmentation ?
L’état K est éclaté en K = O(n / c) partitions appelés « fragments » (shards). Par exemple, un système de fragmentation sur Ethereum peut mettre toutes les adresses commençant par 0x00 dans un fragment, toutes les adresses commençant par 0x01 dans un autre, etc. Dans les formes les plus simples de fragmentation, chaque fragment possède aussi son propre historique des transactions et les effets des transactions dans un fragment k sont limitées à l’état du fragment k. Un exemple simple est celui d’une blockchain multi-actifs où il existe K fragments et où chaque fragment stocke les soldes et traite les transactions associées à un actif particulier. Des formes plus avancées de fragmentation intègrent aussi une forme de communication inter-fragments où des transaction dans un fragment peuvent déclencher des événements dans d’autres fragments.
À quoi pourrait ressembler une conception basique d’une blockchain fragmentée ?
En voici une approche simple. Il existe des nœuds appelés collationneurs (collators) qui acceptent des transactions sur le fragment k (selon le protocole, les collationneurs peuvent choisir quel k ou se voient assigner un k aléatoire) et créent des collations. Une collation comporte un en-tête de collation (collation header), un court message de la forme « Ceci est une collation de transactions sur le fragment k. La racine d’état précédente du fragment k doit être 0x12bc57, la racine de Merkle des transactions de cette collation est 0x3f98ea, et la racine d’état après traitement de ces transactions doit être 0x5d0cc1. Signé, les collationneurs #1, 2, 4, 5, 6, 8, 11, 13 … 98, 99 ».
Un bloc doit donc contenir un en-tête de collation pour chaque fragment. Un bloc est valide si :
- La pré-racine d’état donnée à chaque collation correspond à la racine d’état du fragment associé ;
- Toutes les transactions dans toutes les collations sont valides ;
- La post-racine d’état donnée dans la collation correspond au résultat de l’exécution des transactions de la collation en haut d’un pré-état donné ;
- La collation est signée par au moins les deux tiers des validateurs.
On remarque qu’il existe maintenant plusieurs « niveaux » de nœuds dans un tel système :
- Nœud super-complet – traite toutes les transactions dans toutes les collations et maintient l’état complet de tous les fragments ;
- Nœud de plus haut niveau – traite tous les blocs de plus haut niveau mais ne traite pas ni n’essaye de télécharger les transactions de chaque collation. En revanche, il croit sur parole qu’une collation est valide si plus des deux tiers des collationneurs de ce fragment disent qu’il est valide.
- Nœud de fragment – agit comme un nœud de plus haut niveau mais traite également toutes les transactions et maintient l’état complet d’un fragment donné ;
- Nœud léger – télécharge et vérifie les en-têtes de bloc des blocs de plus haut niveau uniquement ; ne traite pas les en-têtes de collation ni les transactions à moins qu’il n’ait besoin de lire une entrée donnée dans un fragment donné, auquel cas il télécharge la branche de Merkle de l’en-tête de collation le plus récent de ce fragment et, de là, télécharge la preuve de Merkle de la valeur désirée dans l’état.
Quels sont les défis auxquels il faut répondre ?
- Communication inter-fragments – le modèle qui précède ne gère pas les communications inter-fragments. Comment l’ajouter de manière sécurisée ?
- Prises de contrôle d’un fragment – que se faire si un attaquant prend le contrôle d’une majorité des collationneurs d »un fragment donné, que ce soit pour empêcher les collations d’obtenir assez de signatures, pire, pour soumettre des collations invalide ?
- Détection de fraude – si une collation invalide a lieu, comment es nœuds (y compris les clients légers) peuvent-ils en être informés de manière fiable, de sorte qu’ils puissent vérifier la fraude et rejeter la collation si elle est réellement frauduleuse ?
- Problème de disponibilité des données – un sous ensemble de la détection de fraude, que faire quand il manque des données d’une collation ?
- Fragmentation super-quadratique – dans le cas particulier où n > c^2, dans le modèle simple ci-dessus, il y aurait plus de O(c) en-têtes de collations et un nœud ordinaire ne serait donc pas capable de traiter ne serait-ce que les blocs de plus haut niveau. Il en ressort que plus de deux niveaux d’indirection entre les transactions et les en-têtes de blocs de plus haut niveau sont requis (c’est-à-dire que nous avons besoin de « fragments de fragments »). Quelle est la manière la plus simple et la meilleure de mettre cela en œuvre ?
Cependant, l’effet d’une transaction peut dépendre d’évènements qui ont eu lieu auparavant dans d’autres fragments ; un exemple classique est le transfert d’argent où l’argent peut être déplacé du fragment i au fragment j en créant d’abord une transaction de « débit » qui détruit de la monnaie dans le fragment i, puis en créant une transation de « crédit » qui crée de la monnaie dans le fragment j, en pointant vers un reçu créé par la transaction de débit attestant de la légitimité du crédit.
Comment faciliter la communication inter-fragments ?
Dans le scénario le plus simple, il y a beaucoup d’applications qui n’ont chacune pas beaucoup d’utilisateurs et qui n’interagissent que très occasionnellement et de façon très lâche les unes avec les autres ; dans ce cas, les applications peuvent tourner sur des fragments séparés et communiquer entre fragments par reçus (receipts).
Cela implique typiquement de séparer une transaction en un « débit » et un « crédit ». Par exemple, on suppose que nous avons une transaction où le compte A sur le fragment M désire envoyer 100 actifs au compte B sur le fragment N. Les étapes ressembleraient à ce qui suit :
- On envoie une transaction sur le fragment M qui (i) déduit 100 coins du solde de A et (ii) crée un reçu. Un reçu est un objet qui n’est pas directement sauvegardé dans l’état, mais le fait que le reçu a été généré peut être vérifié par une preuve de Merkle.
- On attend que la première transaction soit incluse (on peut demander d’attendre la finalisation, selon le système).
- On envoie la transaction vers le fragment N en incluant une preuve de Merkle du reçu de (1). Cette transaction vérifie aussi dans l’état du fragment N que ce reçu n’est pas « dépensé » ; si c’est le cas, elle augmente le solde de B de 100 coins et écrit dans l’état que le reçu est dépensé.
- De manière facultative, la transaction en (3) écrit également un reçu, qui peut alors être utilisé pour effectuer des actions ultérieures sur le fragment M, subordonnées au succès de l’opérartion d’origine.
Dans des formes plus complexes de fragmentation, les transactions peuvent dans certains cas affecter plusieurs fragments et peuvent également demander des données en synchrone depuis les états d’autres fragments.
Comment différentes sortes d’applications peuvent-elles s’intégrer à une blockchain fragmentée ?
Certaines applications ne demandent absolument aucune interaction entre fragments ; les blockchains multi-actifs et les blockchains avec des applications complètement hétérogènes qui n’exigent aucune interopérabilité, en sont les cas les plus simples. Si des applications ont besoin de communiquer, en revanche, le défi est plus facile à relever si l’interaction peut être asynchrone, c’est-à-dire si l’interaction peut être mise en œuvre en faisant générer un reçu par la transaction sur le fragment A, une transaction sur le fragment B « consommant » ce reçu en effectuant une action en dépendant, et envoyant éventuellement un « callback » au fragment A contenant une réponse. La généralisation de ce modèle est facile et elle n’est pas difficile à intégrer dans un langage de haut niveau.
Notons cependant que les mécanismes internes au protocole qui seraient employés pour des communications inter-fragments asynchrones seraient différents et leurs fonctionnalités seraient réduites par rapport aux mécanismes disponibles pour la communication intra-fragment. Une partie des fonctionnalités actuellement disponibles dans les blockchains classiques ne seraient disponibles, dans une blockchain pouvant passer à l’échelle, que pour la communication intra-fragment[footnote]Si une blockchain classique devient susceptible de passer à l’échelle, la recommandation de l’auteur quant au chemin de migration est que la chaîne de l’ancien état doit simplement devenir un fragment de la nouvelle chaîne/[/footnote].
Quel est le problème de l’avion et de l’hôtel ?
Considérons l’exemple suivant fourni par Andrew Miller. Supposons qu’un utilisateur veuille acheter un billet d’avion et réserver un hôtel, et désire s’assurer que l’opération est atomique – soit les deux réservations sont faites, soit aucune. Si le billet d’avion et la réservation d’hôtel résident sur le même fragment, c’est facile : on crée une transaction qui tente de faire les deux réservations, et qui lève une exception et annule tout à moins que les deux réservation réussissent. Cependant, si elles se trouvent sur des fragments différents, les choses se compliquent ; même sans se préoccuper des aspects crypto-économiques et de la décentralisation, cela revient principalement au problème des transactions atomiques dans les bases de données.
Avec les seuls message asynchrones, la solution la plus simple consiste à réserver d’abord l’avion, puis réserver l’hôtel, puis, une fois que les deux réservations ont réussi, confirmer les deux ; les mécanismes de réservation empêcheraient alors qui que ce soit de réserver (ou du moins s’assurer qu’il reste suffisamment de places pour que toutes les réservations soient confirmées) pendant un certain temps.
Avec les transactions inter-fragments synchrones, le problème est plus facile mais le défi de créer une solution de fragmentation capable de rendre les transactions synchrones atomiques est en soi non trivial.
Si l’usage d’une application donnée dépasse O(c), cette application doit exister sur plusieurs chaînes. La faisabilité dépend des spécificités de l’application elle-même ; certaines (comme les monnaies) sont facilement parallélisables alors que d’autres (certaines formes de marchés) ne peuvent pas l’être et doivent être traitées en série.
Certaines propriétés des blockchains fragmentées s’avèrent impossibles à mettre en œuvre. La https://fr.wikipedia.org/wiki/Loi_d’Amdahl spécifie que dans tout scénario où les applications ont au moins un composant non parallélisable, une fois la parallélisation disponible, le composant non-parallélisable devient rapidement le goulet d’étranglement. Sur une plateforme informatique générique comme Ethereum, il est facile de trouver des exemples de calcul non parallélisable ; un contrat qui garde la trace d’une valeur interne x et qui calcule x = sha3(x, tx_data) en recevant une transaction en est un exemple simple. Aucun système de fragmentation ne peut donner aux applications de ce type une performance supérieure à O(c). Il est donc vraisemblable qu’avec le temps les protocoles de blockchains fragmentées s’amélioreront et seront capables de gérer toujours plus de types d’applications et d’interactions applicatives, mais une architecture fragmentée restera toujours à la traîne d’une architecture à fragment unique au moins sur certains aspects pour des échelles dépassant O(c).
Quels sont les modèles de sécurité au sein desquels opérer ?
Il existe plusieurs modèles concurrents au sein desquels la sécurité des blockchains est évaluée.
- Majorité honnête (ou supermajorité honnête) : on suppose qu’il existe un ensemble de validateurs et jusqu’à ½ (ou ⅓ ou ¼) de ceux-ci sont contrôlés par un attaquant ; le reste des validateurs suit honnêtement le protocole.
- Majorité non coordonnée: on suppose que tous les validateurs sont rationnels au sens de la théorie des jeux (sauf l’attaquant, qui désire créer une défaillance du réseau), mais pas plus d’une certaine fraction (souvent entre ¼ et ½) est capable de coordonner leurs actions.
- Choix coordonné: nous supposons que tous les validateurs sont contrôlés par le même acteur, ou sont pleinement capables de se coordonner sur le choix économiquement optimal. Nous pouvons parler des coûts de la coalition (ou des profits de la coalition) pour arriver à un certain résultat.
- Modèle de l’attaquant corrupteur: nous prenons le modèle de majorité non coordonnée mais, au lieu que l’attaquant soit l’un des participants, celui-ci reste hors du protocole et a la possibilité de soudoyer n’importe quel participant pour changer son comportement. Les attaquants sont modélisés comme ayant un budget, qui est le maximum qu’ils peuvent payer, et nous pouvons parler de leurs coûts, le montant qu’ils finissent par payer pour déséquilibrer le protocole.
La preuve de travail de Bitcoin avec la solution au minage égoïste (selfish mining) de Eyal et Sirer est robuste jusqu’à ½ dans l’hypothèse de la majorité non coordonnée. Shellingcoin reste robuste jusqu’à ½ dans les hypothèses de la majorité honnête et de la majorité non coordonnée, a un coût d’attaque de ε (c’est-à-dire légèrement supérieur à zéro) dans un modèle de choix coordonné, et demande un budget de P + ε et un coût de ε dans un modèle d’attaquant corrupteur en raison des attaques P + epsilon.
Il existe aussi des modèles hybrides ; par exemple, même dans les modèles de choix coordonné et d’attaquant corrupteur, il est courant de faire une hypothèse de minorité honnête où une partie (peut-être entre 1 et 15%) des validateurs agissent de manière altruiste quelles que soient les incitations. Nous pouvons alors parler des coalitions rassemblant entre 50 et 99% des validateurs qui essayent de déstabiliser le protocole ou de nuire à d’autres validateurs par exemple, dans la preuve de travail, une coalition de 51% peut doubler ses revenus en refusant d’inclure les blocs de tous les autres mineurs.
Le modèle de la majorité honnête est indiscutablement irréaliste et a déjà été réfuté empiriquement : en guise d’exemple pratique, voir le fork de minage SPV de Bitcoin. Il prouve trop : par exemple, un modèle de majorité honnête impliquerait que des mineurs honnêtes sont disposés à brûler leur propre argent si cela permet de punir les attaquants d’une manière ou d’une autre. L’hypothèse de la majorité non coordonnée peut être réaliste ; il existe aussi un modèle intermédiaire où la majorité des nœuds est honnête mais dispose d’un budget, et l’attaquant arrête s’il commence à perdre trop d’argent.
Le modèle de l’attaquant corrupteur a été critiqué dans certains cas pour son agressivité irréaliste, bien que ses partisans soutiennent que si un protocole est conçu dans l’esprit du modèle de l’attaquant corrupteur, il devrait pouvoir réduire massivement le coût du consensus puisque des attaques à 51% deviennent des évènements dont on peut réchapper. Nous évaluerons la fragmentation aussi bien dans le contexte de la majorité non coordonnée que dans celui du modèle de l’attaquant corrupteur.
Comment peut-on parer à l’attaque de prise de contrôle d’un fragment dans un modèle de majorité non coordonnée ?
En deux mots, échantillonnage aléatoire. Chaque fragment se voit assigner un certain nombre de collationneurs (par exemple 150) et le validateur qui fait un bloc sur chaque fragment est pris dans l’échantillon de ce fragment. Les échantillons peuvent être tirés à nouveau soit semi-fréquemment (comme une fois toutes les 12 heures) soit extrêmement fréquemment (il n’y a pas de processus d’échantillonnage réellement indépendant, les collationneurs sont sélectionnés aléatoirement pour chaque fragment depuis un pool global à chaque bloc).
Il en résulte que même alors que seuls quelques nœuds vérifient et créent les blocs sur chaque fragment à un instant donné, le niveau de sécurité n’est en fait pas très amoindri dans un modèle de majorité honnête/non coordonnée par rapport à une situation où chaque nœud vérifie et crée des blocs. C’est une simple question de statistiques : si l’on suppose une supermajorité de ⅔ dans l’ensemble global et si la taille de l’échantillon est de 150, il y a une probabilité de 99,999% que la condition de majorité honnête soit satisfaite dans l’échantillon. Si l’on suppose une super-majorité honnête de ¾ dans l’ensemble global, alors cette probabilité passe à 99.999999998% (voir ici les détail du calcul).
Il en découle que, au moins dans la configuration d’une majorité honnête/non coordonnée, nous avons :
- Décentralisation (chaque nœud ne stocke que O(c) données car il est client léger dans O(c) fragment et stocke donc O(1) * 0(c) = O(c) donnée d’en-têtes de blocs, ainsi que O(c) données correspondant à l’état complet et l’historique récent d’un ou plusieurs fragments auxquels il est assigné actuellement) ;
- Passage à l’échelle (avec O(c) fragments, chacun ayant une capacité de O(c), la capacité maximale est de n = O(c^2)) ;
- Sécurité (les attaquants doivent contrôler au moins ⅓ de tout le pool de validateurs pour avoir une chance de prendre le contrôle du réseau.
Dans le modèle de Zamfir (ou bien dans le modèle de l’« adversaire très très adaptatif »), tout n’est pas si simple mais nous y viendrons plus tard. Notons qu’en raison des imperfections de l’échantillonnage, le seuil de sécurité décroît de ½ à ⅓, mais cette perte de sécurité reste étonamment basse pour un gain potentiel de 100 à 1000x en passage à l’échelle sans perte de décentralisation.
Comment faire concrètement cet échantillonnage en preuve de travail, et en preuve d’enjeu ?
En preuve d’enjeu, c’est facile. Il existe déjà un « ensemble de validateurs actifs » dont on garde la trace dans l’état et on peut simplement prendre directement un échantillon depuis cet ensemble. Soit un algorithme interne au protocole est lancé pour choisir 150 validateurs pour un fragment, soit chaque validateur lance indépendamment un algorithme utilisant une source commune de hasard pour déterminer (incontestablement) dans quel fragment il se trouve à un instant donné. Remarquons qu’il est très important que l’assignation de l’échantillon soit « obligatoire » ; les validateurs n’ont pas le choix de leur fragment. Si les validateurs pouvaient choisir, des attaquants avec une petite somme en jeu pourraient concentrer leur mise sur un fragment et l’attaquer, éliminant de ce fait la sécurité du système.
En preuve de travail, c’est plus difficile car, dans les systèmes de preuve de travail « directe », on ne peut pas empêcher les mineurs d’appliquer leur travail à un fragment donné. Il doit être possible d’employer les formulaires de preuve d’accès aux fichiers de la preuve de travail pour verrouiller chaque mineur dans un fragment donné mais il est difficile d’être sûr que les mineurs ne peuvent pas rapidement télécharger et générer des données pouvant être utilisées pour d’autres fragments et donc contourner ce mécanisme. La meilleure approche connue dans ce domaine est une technique inventée par Dominic Williams appelée les « tours de puzzle » où les mineurs effectuent d’abord une preuve de travail sur une chaîne commune, qui les conduit dans un pool de validateurs un peu comme dans la preuve d’enjeu, et le pool de validateurs est échantillonné tout comme en preuve d’enjeu.
Une piste intermédiaire possible pourrait ressembler à ce qui suit. Les mineurs peuvent dépenser une grande quantité (de taille O(c)) de travail pour créer une nouvelle « identité cryptographique ». La valeur précise de la solution de preuve de travail choisit ensuite de quel fragment ils disposent sur lequel ils feront leur prochain bloc. Ils peuvent ensuite dépenser une quantité de travail équivalente à O(1) pour créer un bloc sur ce fragment, et la valeur de cette solution de preuve de travail détermine sur quel fragment ils peuvent travailler ensuite, et ainsi de suite[footnote]Pour que ce soit sûr, quelques autres conditions doivent être satisfaites ; en particulier, la preuve de travail ne peut être externalisable afin d’empêcher l’attaquant de déterminer quelles autres identités de mineurs sont disponibles pour un fragment donné afin de miner au-dessus de celles-ci.[/footnote]. Notons que toutes ces approches rendent la preuve de travail d’une certaine manière « stateful », qu’elles impliquent une mémoire de l’état ; cette nécessité est fondamentale.
Quels sont les compromis nécessaires pour un échantillonnage plus ou moins fréquent ?
La fréquence de sélection dépend simplement de la nature adaptative des adversaire auxquels le réseau doit faire face pour rester sûr. Par exemple, si l’on croit qu’une attaque adaptative (comme des validateurs malhonnêtes qui découvrent qu’ils font partie du même échantillon et qui se regroupent en coalition) peut se produire en 6 heures mais pas moins, alors un temps d’échantillonnage de 4 heures conviendrait mais pas de 12 heures. C’est un argument en faveur d’un échantillonnage aussi fréquent que possible.
Le défi principal de l’échantillonnage à chaque bloc est que le tirage au sort implique une très grande quantité de travail supplémentaire. En particulier, la vérification d’un bloc sur un fragment demande de connaître l’état de ce fragment, et donc à chaque fois que les validateurs sont tirés au sort, ceux-ci doivent télécharger la totalité de l’état du nouveau fragment dans lequel ils se trouvent. Cela demande à la fois une politique de contrôle étroit de la taille de l’état (en s’assurant économiquement que la taille de l’état ne croît pas trop, que ce soit en supprimant les anciens comptes, en restreignant le taux de création de nouveaux comptes ou une combinaison des deux) et un temps de tirage au sort assez long pour bien fonctionner.
Actuellement, le client Parity peut télécharger et vérifier un snapshot, un instantané d’état Ethereum complet par « warp-sync » en ~3 minutes ; si nous augmentons de 20x pour compenser un usage croissant (10 tx/sec au lieu de l’actuel 0,5 tx/sec) (nous supposons que les politiques de contrôle de la taille de l’état à venir et la « poussière » (dust) due à l’usage sur le long terme ont tendance à s’annuler), nous obtenons un temps de synchronisation de l’état de 60 minutes, ce qui suggère que des périodes de 12-24 heures mais pas moins sont sûres.
Il y a deux voies possibles pour affronter ce défi.
Peut-on forcer à détenir plus d’état côté utilisateur pour que les transactions puissent être validées sans demander aux validateurs de détenir toutes les données d’état ?
Ces techniques demandent aux utilisateurs de stocker des données d’état et de fournir des preuves de Merkle avec toutes les transactions qu’ils envoient. Une transaction serait envoyée avec une preuve de Merkle d’exécution correcte et cette preuve permettrait à un nœud ne possédant que l’état racine de calculer un nouvel état racine. Elle comprend le sous-ensemble des objets du trie qui doivent être traverséss pour accéder aux informations que la transaction doit vérifier ; comme les preuves de Merkle sont de taille O(log(n)), la preuve d’une transaction qui accède à un nombre constant d’objets serait également de taille O(log(n)).
Le sous-ensemble d’objets dans un arbre de Merkle qui devrait être fourni dans la preuve de Merkle d’une transaction accédant à plusieurs objets d’état
L’implémentation de ce système sous sa forme la plus pure a deux défauts. D’abord, elle introduit une surcharge O(log(n)), bien que l’on puisse soutenir que cette dernière ne soit pas si énorme que ce qu’il y paraît car elle garantit que le validateur peut se contenter de conserver les données d’état en mémoire, donc sans jamais impliquer d’accéder au disque[footnote] Les récentes attaques par déni de service sur Ethereum ont prouvé que l’accès au disque dur est un goulet d’étranglement crucial pour le passage à l’échelle d’une blockchain.[/footnote]. Ensuite, elle peut facilement être appliquée si les objets d’état auxquels on accède dans une transaction sont statiques, ce qui est en revanche plus difficile si les objets en question sont dynamiques – c’est-à-dire si l’exécution de la transaction comporte du code de la forme read(f(read(x))) où l’adresse d’une lecture d’état dépend du résultat de l’exécution d’une autre lecture d’état. Dans ce cas, l’adresse que l’émetteur de la transaction pense que celle-ci va lire au moment de l’envoi peut très bien différer de celle qui est en fait lue quand la transaction est incluse dans un bloc et la preuve de Merkle peut s’avérer insuffisante[footnote]Vous pouvez demander : eh bien pourquoi les validateurs ne récupèrent-ils pas les preuves de Merkle au fil de l’eau ? Réponse : Parce que c’est une étape de ~100-1000 ms, et l’exécution de l’intégralité d’une transaction complexe pendant ce laps de temps peut être prohibitive.[/footnote].
Un compromis consiste à permettre aux émetteurs de transactions d’envoyer une preuve qui incorpore les données auxquelles on aura le plus probablement besoin d’accéder ; si la preuve est suffisante, la transaction est acceptée et, si l’état change inopinément, la preuve devient insuffisante et l’expéditeur devrait alors renvoyer la transaction, à moins qu’une sorte de nœud d’assistance sur le réseau la renvoie en ajoutant la preuve correcte. Les développeurs seraient alors libres d’effectuer des transactions dont le comportement serait dynamique mais, plus celui-ci serait dynamique, moins les transactions pourraient être incluses dans des blocs.
Remarquons que les stratégies d’inclusion de transaction de la part des validateurs dans ce cadre seraient nécessairement compliquées car il peuvent dépenser des millions en gaz pour traiter une transaction, pour se rendre finalement compte que la dernière étape accède à une entrée d’état dont ils ne disposent pas. Un compromis possible est que les validateurs peuvent avoir une stratégie qui n’accepte que (i) les transactions avec un coût en gaz très bas, comme <100k, et (ii) les transactions qui spécifient un ensemble statique de contrats auxquelles elles ont le droit d’accéder et qui contiennent les preuves de tout l’état de ces contrats. Notons que cela ne s’applique qu’au moment de la diffusion initiale de ces contrats ; une fois une transaction incluse dans un bloc, l’ordre d’exécution est fixé et donc seule la preuve de Merkle minimal correspondant à l’état auquel on doit réellement accéder peut être fourni.
Si les validateurs ne sont pas immédiatement à nouveau tirés au sort, il y a une nouvelle opportunité d’augmenter l’efficience. Nous pouvons attendre des validateurs qu’ils stockent les données des preuves de transactions qui ont déjà été traitées, afin que ces données n’aient pas à être renvoyées ; si k transactions sont envoyées pendant une période de tirage au sort, cela abaisse e la taille moyenne d’une preuve de Merkle de log(n) à log(n) – log(k).
Comment l’aléa de l’échantillonnage aléatoire est-il généré ?
Tout d’abord, il faut noter que, même si une génération de nombre aléatoire est massivement exploitable, ce n’est pas un défaut fatal pour le protocole ; cela signifie simplement qu’il y a un support pour une grande incitation à la centralisation. En effet, comme l’aléa choisit dans des échantillons assez vastes, il est difficile de biaiser le hasard sur plus qu’un certain montant.
La manière la plus simple de le démontrer passe par la distribution binomiale, décrite ci-dessus ; si l’on désire éviter qu’un échantillon de taille N supérieure à 50% ne soit corrompu par un attaquant, et si un attaquant a p% des mises globales, la chance qu’un attaquent soit en mesure d’obtenir une telle majorité pendant un tour est :
Voici un tableau résumant ce que cette probabilité devient en pratique pour diverses valeurs de N et de p :
<
| N = 50 | N = 100 | N = 150 | N = 250 | |
| p = 0.4 | 0.0978 | 0.0271 | 0.0082 | 0.0009 |
| p = 0.33 | 0.0108 | 0.0004 | 1.83 * 10-5 | 3.98 * 10-8 |
| p = 0.25 | 0.0001 | 6.63 * 10-8 | 4.11 * 10-11 | 1.81 * 10-17 |
| p = 0.2 | 2.09 * 10-6 | 2.14 * 10-11 | 2.50 * 10-16 | 3.96 * 10-26 |
Donc, pour N >= 150, la probabilité qu’une graine d’aléa donnée mène à un échantillon favorisant l’attaquant est vraiment très petite[footnote] Une solution hybride qui combine l’efficience habituelle des petits échantillons avec la robustesse accrue d’échantillons plus grands est un système d’échantillonnage multicouches : avec un consensus entre 50 nœuds qui demande un agrément de 80% pour poursuivre, et si et seulement si ce consensus échoue à être atteint, revenir à un échantillon de 250 nœuds. N = 50 avec un seuil de 80% n’a qu’un taux d’échec de 8,92 * 10-9 même contre des attaquants avec p = 0,4, donc la sécurité n’est pas mise à mal dans un modèle de majorité honnête ou non coordonnée.[/footnote],[footnote]Les probabilités données sont pour un fragment unique ; cependant, la graine d’aléa affecte O(c) fragments et l’attaquant pourrait potentiellement prendre le contrôle de l’un quelconque d’entre eux. Si nous voulons examiner simultanément O(c) fragments, deux cas se présentent. D’abord, si le processus de grinding est informatiquement limité, alors ce fait ne change rien au calcul puisque, même s’il y a maintenant O(c) chances de succès par round, la vérification de la réussite prend O(c) fois plus de travail. Ensuite, si le processus de grinding est économiquement limité, alors cela demande effectivement des facteurs de sûreté nettement plus importants (l’augmentation de N par 10 ou 20 devrait suffire) bien qu’il soit important de noter que le but d’un attaquant dans une attaque par manipulation motivée par le profit est d’augmenter sa participation à tous les fragments dans tous les cas et donc c’est le problème que nous étudions déjà.[/footnote]. Du point de vue de la sécurité de l’aléa, cela signifie que l’attaquant doit avoir une liberté maximale dans le choix de l’ordre des valeurs aléatoires pour casser complètement le processus d’échantillonnage. La plupart des vulnérabilités touchant l’aléa en preuve d’enjeu ne permettent pas à l’attaquant de choisir simplement une graine ; au pire, elles lui donnent plusieurs chances de choisir la graine la plus favorable parmi plusieurs choix générés de manière pseudo-aléatoire. Si cela est un sujet de forte inquiétude, on peut simplement augmenter la valeur de N et ajouter une fonction de dérivation de clef modérément complexe au processus de calcul de l’aléa de sorte qu’il faille plus de 2100 étapes pour trouver le moyen de suffisamment biaiser l’aléa.
Passons maintenant au risque d’attaques essayant d’influencer l’aléa de manière plus marginale, pour le profit plus que pour une prise de contrôle complète. Par exemple, supposons qu’il existe un algorithme qui sélectionne de manière pseudo-aléatoire 1000 validateurs à partir d’un ensemble très vaste (chaque validateur gagnant 1$), qu’un attaquant ait 10% des mises et que son revenu « honnête » moyen soit donc de 100$ et que, pour un coût de 1$, l’attaquant puisse manipuler l’aléa pour « re-tirer les cartes » (et l’attaquant peut le faire un nombre illimité de fois).
En raison du théorème central limite, de la déviation standard du nombre d’échantillons, et en se fondant sur d’autres résultats connus en mathématiques, le maximum attendu de N échantillons aléatoires se trouve légèrement sous M + S * sqrt(2 * log(N)) où M est la moyenne et S est la déviation standard. La récompense issue de la manipulation de l’aléa et du rejeu des dés (c’est-à-dire l’accroissement de N) chute brutalement. Par exemple avec 0 réessais la récompense espérée est de 100$, avec 1 réessai elle est de 105,5$, avec deux elle est de 108,5$, avec trois elle est de 110,3$, avec quatre elle est de 111,6$, avec cinq elle est de 112,6$ et avec six de 113,5$. Donc, après cinq réessais, ce n’est plus intéressant. Il en résulte qu’un attaquant économiquement motivé avec dix pour cent des mises dépensera (avec un coût social) 5$ pour un gain supplémentaire de 13$, pour un bénéfice net de 8$.
Cependant, ce genre de raisonnement supppose qu’un seul rejeu des dés soit coûteux. De nombreux anciens algorithmes de preuve d’enjeu ont une vulnérabilité de stake grinding où relancer les dés signifie simplement effectuer un calcul sur son ordinateur ; les algorithmes comportant cette vulnérabilité sont bien sûr inacceptables dans un contexte de fragmentation. Les nouveaux algorithmes (voir la section sur la sélection des validateurs dans la FAQ de la preuve d’enjeu) font en sorte que le rejeu implique d’abandonner sa place dans le processus de création de bloc, avec les récompenses et les frais associés. La mailleure manière d’atténuer l’impact d’attaques marginales économiquement motivées sur la sélection des échantillons consiste à trouver le moyen d’augmenter ce coût. On peut l’augmenter d’un facteur de sqrt(N) depuis N tours de vote par la méthode des bits de majorité d’Iddo Bentov ; l’algorithme de fragmentation du Mauve Paper devrait utiliser cette approche.
Une autre forme de génération de nombre aléatoire, qui n’est pas exploitable par des coalitions minoritaires, et l’approche de la signature à seuil variable étudiée et soutenue par Dominic Williams. La stratégie consiste à utiliser une signature à seuil déterministe pour générer la graine d’aléa servant à sélectionner les échantillons. Ces signatures ont comme propriété de garantir qu’une valeur reste la même, peu importe qui d’un ensemble de participant fournit des données à l’algorithme, pourvu qu’au moins ⅔ des participants soient honnêtes. Cette approche est plus évidemment inexploitable économiquement, et totalement résistant à toutes les formes de stake grinding, mais elle comporte plusieurs faiblesses :
- Elle dépend d’une cryptographie complexe (en particulier les courbes et les appariements elliptiques). D’autres approches ne se fondent que sur l’hypothèse d’un oracle aléatoire pour les algorithmes de hachage habituels.
- Elle échoue quand beaucoup de validateurs sont hors ligne. L’un des buts souhaités pour les blockchains publiques est de pouvoir survivre à la disparition simultanée de grandes parties du réseau, tant que la majorité des nœuds reste honnête ; les systèmes de signature à seuil déterministe ne peuvent fournir cette propriété actuellement.
- Elle n’est pas aussi sûre dans un modèle de Zamfir où plus des ⅔ des validateurs complotent. Les autres approches décrites dans la FAQ de la preuve d’enjeu rendent toujours coûteuse la manipulation de l’aléa, car les données de tous les validateurs sont mélangées dans la graine et toute manipulation demande soit une collusion universelle, soit l’exclusion totale des autres validateurs.
On peut arguer de ce que l’approche des signatures à seuil déterministe fonctionne mieux dans des contextes favorisant la cohérence et que les autres approches fonctionnent mieux dans des contextes favorisant la disponibilité.
Quels sont les préoccupations en rapport avec la fragmentation par échantillonnage aléatoire dans un modèle de Zamfir ?
Dans le modèle de l’attaquant corrupteur ou celui du choix coordonné, le fait que les validateurs sont échantillonnés aléatoirement n’a pas d’importance : quel que soit l’échantillon, soit l’attaquant peut corrompre la grande majorité de l’échantillon pour faire ce qui lui plaît, soit il contrôle directement une majorité de l’échantillon et peut le diriger pour effectuer des actions à bas coût (O(c), pour être précis).
À ce point, l’attaquant peut conduire des attaques à 51% contre cet échantillon. La menace est aggravée par le risque de contagion inter-fragment : si l’attaquant corrompt l’état d’un fragment, il peut alors commencer à envoyer des quantités illimitées de fonds vers d’autres fragments, entre autres forfaits. L’un dans l’autre, la sécurité des modèles de l’attaquant corrupteur et du choix coordonné n’est pas meilleure que celle de la création de O(c) altcoins.
Comment peut-on améliorer la situation ?
Essentiellement en résolvant le problème de la détection de fraude.
Une des principales catégories de solution à ce problème est l’utilisation de mécanismes de défi-réponse. Les mécanismes de défi-réponse se fondent généralement sur un principe d’escalade : le fait X (c’est-à-dire « la collation n° 17293 du fragment n° 54 est valide ») est initialement accepté comme vrai si au moins k validateurs signent une déclaration (confirmée par un dépôt) en ce sens. Cependant, si cela se produit, il y a une période de défi pendant laquelle 2k validateurs peuvent signer une déclaration selon laquelle elle est fausse. Dans ce cas, 4k validateurs peuvent signer une déclaration selon laquelle elle est en fait fausse, et ainsi de suite jusqu’à ce qu’un des côtés abandonne ou que la plupart des validateurs aient signé des déclarations, à quel point chaque validateur vérifie par lui-même si X est vrai ou faux. Si X est jugé vrai, chacun ayant déclaré en ce sens est récompensé et chacun ayant déclaré en l’autre sens est pénalisé, et vice versa.
Avec ce mécanisme, on peut prouver que les acteurs malveillants perdent un montant proportionnel au nombre d’acteurs qu’ils ont forcé à vérifier la véracité de X ; cela empêche d’utiliser le système comme un vecteur de déni de service. Ce système peut être implémenté d’une manière ainsi structurée, ou bien sous une forme plus libre par un marché de prédiction. Le système de finalité du Mauve Paper s’oriente vers cette dernière solution.
Quel est le problème de la disponibilité des données, et comment peut-on utiliser les codes à effacement pour le résoudre ?
Voir https://github.com/ethereum/research/wiki/A-note-on-data-availability-and-erasure-coding.
Cela signifie-t-il qu’il est possible de créer des blockchains fragmentées susceptibles de passer à l’échelle où le coût d’une malveillance est proportionnelle à la taille de tout l’ensemble des validateurs ?
Il existe une attaque triviale par laquelle un attaquant peut toujours brûler un capital de O(c) pour réduire temporairement la qualité d’un fragment : il le spamme en envoyant des transactions avec des frais très importants, forçant ainsi les utilisateurs légitimes à surenchérir pour rentrer. Cette attaque est inévitable ; on peut la compenser par des limites de gaz souples, et on peut même essayer des systèmes de « fragmentation transparente » qui essaient de réallouer automatiquement des nœuds à des fragments selon l’usage mais, si une application donnée est non-parallélisable, la loi d’Amdahl garantit qu’on n’y peut rien. L’attaque qui est décrite ici (rappel : cela ne fonctionne qu’avec le modèle de Zamfir, et non avec une majorité honnête/non coordonnée) est évidemment bien pire que l’attaque par spam de transactions. Nous savons donc que nous avons atteint la limite connue pour la sécurité d’un fragment donné et il ne sert à rien d’aller plus loin.
Revenons un peu en arrière. A-t-on réellement besoin de cette complexité avec un tirage instantané ? Dans ce cas, cela ne signifie-t-il pas que chaque fragment tire directement les validateurs du pool global de validateurs et qu’il se comporte comme une blockchain, et donc que la fragmentation n’introduit pas de nouvelle complexité ?
En quelque sorte. Tout d’abord, il faut noter que la preuve de travail et la preuve d’enjeu simple, même sans fragmentation, ont toutes les deux une sécurité très faible dans un modèle de Zamfir ; un bloc n’est vraiment « finalisé » dans le sens zamfirien qu’après un temps O(n) (si seulement quelques blocs ont passé, alors le coût économique de remplacement de la chaîne est simplement le coût de démarrage d’une double dépense à partir d’avant le bloc en question). Casper résoud ce problème en ajoutant son mécanisme de finalité afin que la marge de sécurité économique augmente immédiatement vers le maximum. Dans une chaîne fragmentée, si nous voulons la finalité économique, alors nous devons concevoir une chaîne de raisonnement telle qu’un validateur puisse en venir à faire une déclaration très forte sur une chaîne en se fondant uniquement sur un échantillon quelconque, quand le validateur lui-même est convaincu que les modèles de l’attaquant corrupteur et du choix coordonné peuvent être corrects et donc que l’échantillon en question pourrait être corrompu.
Vous avez parlé de fragmentation transparente. J’ai 12 ans, qu’est-ce que c’est ?
En gros, le concept de « fragment » n’est pas directement exposé aux développeurs et il n’est pas assigné d’objets d’état aux fragments. Le protocole possède un processus d’équilibrage de charge intégré qui déplace les objets d’un fragment à l’autre. Si fragment devient trop gros ou consomme trop de gaz, il peut être éclaté en deux ; si deux fragments deviennent trop petits et communiquent souvent, ils peuvent être combinés en un seul ; si tous les fragments deviennent trop petits, un fragment peut être supprimé et son contenu déplacé vers d’autres fragments, etc.
Imaginez que Donald Trump se rende compte que les gens voyagent beaucoup entre New York et Londres, mais qu’il y a un océan en travers. Il se contenterait alors de sortir ses ciseaux, de découper l’océan, de coller la côte est des États-Unis à l’Europe occidentale et de mettre l’Atlantique derrière le Pôle Sud… quelque chose comme ça.
Quels en sont les avantages et les inconvénients ?
- Les développeurs n’ont plus besoin de penser aux fragments ;
- Les fragments ont la possibilité de s’ajuster manuellement aux variations des prix du gaz au lieu de dépendre des mécanismes de marché pour augmenter le prix du gaz dans certains fragments plus que dans d’autres ;
- Il n’y a plus de notion fiable de cohabitation : si deux contrats sont placés dans le même fragment afin qu’ils puissent interagir l’un avec l’autre, les modifications de fragments peuvent très bien les séparer ;
- Plus de complexité protocolaire.
Le problème de la cohabitation peut être atténué par l’introduction d’une notion de « domaines séquentiels » où les contrats peuvent spécifier qu’ils existent dans le même domaine séquentiel, auquel cas la communication synchrone entre eux sera toujours possible. Dans ce modèle, un fragment peut être vu comme un ensemble de domaines séquentiels validés ensemble, où des domaines séquentiels peuvent être rééquilibrés entre fragments si le protocole détermine une meilleure efficience dans ce cas.
Comment fonctionneraient des messages inter-fragments ?
Le processus devient bien plus facile quand on regarde l’historique des transactions comme étant déjà réglé et quand on essaie simplement de calculer la fonction de transition d’état. Plusieurs approches sont possibles ; l’une d’entre elles, assez simple, peut être décrite comme suit :
- Une transaction peut spécifier un ensemble de fragments sur lequel il peut opérer ;
- Afin que la transaction soit effective, elle doit être incluse à la même hauteur de bloc dans tous ces fragments ;
- Les transactions dans un bloc doit être mises dans l’ordre de leurs empreintes (ce qui assure un ordre d’exécution convenable).
Un client sur le fragment X, s’il voit une transaction sur les fragments (X, Y), demande une preuve de Merkle au fragment Y vérifiant (i) la présence de cette transaction sur le fragment Y, et (ii) quel est le pré-état sur le fragment U pour ces bits de données auxquels la transaction devra accéder. Elle exécute alors la transaction et s’engage sur le résultat de l’exécution. Remarquons que ce processus peut être très inefficace s’il y a de nombreuses transactions avec des « appariements de blocs » différents dans chaque bloc ; c’est pourquoi il peut être optimal de se contenter d’exiger des blocs qu’ils spécifient des fragments frères, après quoi le calcul peut être lancé de manière plus performante. Voici donc la base d’un fonctionnement possible d’un tel système ; on pourrait en imaginer de plus complexes. Cependant, quand on conçoit un nouveau système, il est toujours important de s’assurer que des attaques par déni de service peu coûteuses ne peuvent pas ralentir le calcul de l’état.
Et les messages semi-synchrones ?
Vlad Zamfir a créé un système par lequel des messages asynchrones pouvaient quand même résoudre le problème de la « réservation d’un train et d’un hôtel ». Voici comment. L’état garde la trace de toutes les opérations ayant été récemment effectuées, ainsi que le graphe des opérations qui ont été déclenchées par une autre opérations (y compris inter-fragments). Si une opération est annulée, un reçu est créé qui peut alors être utilisé pour annuler tout effet de cette opération sur les autres fragments ; ces annulations peuvent alors en déclencher d’autres et ainsi de suite. L’argument ici est que si l’on biaise le système de manière à ce que des messages d’annulation puissent se propager deux fois plus vite que les autres messages, alors une transaction inter-fragments complexe qui finit de s’exécuter en K étapes peut être totalement annulée en K autres étapes.
Il est clair que la surcharge introduite par ce système a été insuffisamment étudiée ; on peut rencontrer des scénarios catastrophes qui déclenchent des vulnérabilités d’exécution quadratique. Bien sûr, si des transactions ont des effets plus isolés que d’autres, la surcharge de ce mécanisme est inférieure ; des exécutions isolées pourraient éventuellement être incitées via des règles de coût en gaz favorables. L’un dans l’autre, il s’agit d’une des directions les plus prometteuses pour la recherche sur la fragmentation avancée.
Que sont les appels inter-fragments garantis ?
L’un des défis de la fragmentation est que, quand un appel est lancé, il n’existe par défaut aucune garantie certaine fournie par le protocole qu’une opération asynchrone créée par cet appel sera effectuée dans un laps de temps donné, ou même sera faite tout court ; il appartient à une tierce partie d’envoyer une transaction au fragment de destination déclenchant le reçu. Cela convient à de nombreuses applications mais peut s’avérer problématique dans certains cas pour plusieurs raisons :
- Il se peut qu’aucune partie ne soit clairement incitée à déclencher un reçu donné. Si l’envoi d’une transaction bénéficie à plusieurs parties, alors il peut se produire des effets de tragédie des biens communs où les parties essaient de se défiler en attendant que quelqu’un d’autre envoie la transaction, ou décident simplement que l’envoi de la transaction ne vaut pas les frais de transaction.
- Le prix du gaz peut varier d’un fragment à l’autre et, dans certains cas, la première partie d’une opération contraint l’utilisateur à donner suite, mais celui-ci peut du coup souffrir d’un prix du gaz bien supérieur. Cela peut être exacerbé par des attaques par déni de service et d’autres formes d’agression.
- Certaines applications comptent sur une limite supérieure à la « latence » des messages inter-fragments (comme dans l’exemple du train et de l’hôtel). En l’absence de garanties absolues, ces applications devraient mettre en place des marges de sécurité d’une taille rédhibitoire.
On pourrait essayer de concevoir un système où les messages asynchrones provenant d’un fragment déclenchent automatiquement des effets dans leur fragment de destination après un certain nombre de blocs. Cependant, cela demande que chaque client sur chaque fragment inspecte activement tous les autres fragments au cours du processus de calcul de la fonction de transition d’état, ce qui est indiscutablement une source d’inefficacité. La meilleure approche connue de compromis est celle-ci : quand un reçu du fragment A à la hauteur height_a est inclus dans le fragment B à la hauteur height_b, si la différence en hauteur de bloc dépasse MAX_HEIGHT, alors tous les validateurs du fragment B qui ont créé des blocs depuis height_a + MAX_HEIGHT + 1 jusqu’à height_b – 1 sont pénalisés et cette pénalité augmente exponentiellement. Une partie de ces pénalités est donnée au validateur qui a fini par inclure le bloc en tant que récompense. La fonction de transition d’état reste ainsi simple tout en incitant fortement à un comportement correct.
Attendez, et si un attaquant envoyait un appel inter-fragments depuis tous les fragments vers le fragment X au même moment ? Ne serait-il pas mathématiquement impossible d’inclure tous ces appels en temps voulu ?
Correct ; c’est un vrai problème. Voici une proposition de solution. Afin de lancer un appel inter-fragments du fragment A au fragment B, l’appelant doit d’abord acheter du « gaz B congelé » (ce qui est fait par une transaction dans le fragment B, et enregistré dans le fragment B). Le gaz congelé du fragment B a un taux de demeurage rapide : une fois commandé, il perd 1/k de sa valeur à chaque bloc. Une transaction sur le fragment A peut alors envoyer le gaz B congelé avec le reçu qu’il crée, et il peut être gratuitement utilisé sur le fragment B. Les blocs du fragment B allouent un espace de gaz supplémentaire spécifiquement pour ces transactions. Notons qu’en raison des règles de demeurage, il ne peut y avoir au plus que pour GAS_LIMIT * k de gaz congelé disponible pour un fragment donné à tout moment, qui peut être certainement rempli pendant k locs (en fait, encore plus vite en raison du demeurage, mais nous avons besoin de cet espace libre en raison des validateurs malveillants). Au cas où trop de validateurs échouent de manière malveillante à inclure les reçus, nous pouvons rendre les pénalités plus justes en exemptant les validateurs qui remplissent l’« espace de reçus » de leurs blocs avec autant de reçus que possible, en commençant par les plus anciens.
Selon ce mécanisme de pré-achat, un utilisateur qui désire effectuer une opération inter-fragments doit d’abord acheter à l’avance du gaz pour tous les fragments nécessaires à l’opération, en prévoyant une marge pour le demeurage. Si l’opération crée un reçu qui déclenche une opération consommant 100000 gaz dans le fragment B, l’utilisateur achète 100000 * e (ie. 271818) de gaz congelé du fragment B. Si cette opération consomme à son tour 100000 gaz dans le fragment C (avec deux niveaux d’indirection), l’utilisateur doit pré-acheter 100000 * e^2 (ie. 738906) de gaz congelé du fragment C. Remarquons que, une fois les achats confirmés, quand l’utilisateur commence l’opération principale, celui-ci peut être sûr qu’il sera isolé des variations du marché du gaz, à moins que des validateurs ne perdent volontairement de grandes sommes d’argent en pénalités de non-inclusion de reçus.
Du gaz congelé ? Ça a l’air intéressant non seulement pour les opérations inter-fragments mais aussi assez fiable pour l’ordonnancement intra-fragment.
Tout à fait ; on peut acheter du gaz congelé à l’intérieur du fragment A et lancer un appel inter-fragment depuis le fragment A vers lui-même. Notons cependant que ce système ne supporterait que l’ordonnancement sur des intervalles très courts et qu’il ne garantirait pas l’exécution pour le bloc courant, mais que celle-ci se produirait à coup sûr que dans un bref laps de temps.
L’ordonnancement garanti, qu’il soit intra-fragment ou inter-fragments, ne peut-il pas servir contre les collusion majoritaires essayant de censurer les transaction ?
En effet. Si un utilisateur échoue à faire passer une transaction parce qu’une collusion de validateurs filtre la transaction et n’accepte aucun bloc la contenant, alors il peut envoyer une série de messages qui déclenchent une chaîne de messages dont l’ordonnancement est garanti et dont le dernier reconstruit la transaction à l’intérieur de l’EVM pour l’exécuter. Il est pratiquement impossible d’empêcher ces techniques de contournement sans arrêter net la fonctionnalité d’ordonnancement garanti et des validateurs malveillants ne pourraient pas le faire facilement.
Les blockchains fragmentées permettraient-elle de mieux gérer les partitions réseau ?
Les systèmes décrits dans ce document n’offriraient aucune amélioration par rapport aux blockchains non fragmentées ; soyons réalistes, tous les fragments finiraient avec des nœuds de chaque côté de la partition. Il y a eu des appels (par exemple de Juan Benet de IPFS) à concevoir des réseaux capables de passer à l’échelle, dont la caractéristique spécifique est de pourvoir être éclatés en fragments à la demande et donc de pouvoir continuer à fonctionner autant que possible dans des conditions de partitionnement réseau, mais leur fonctionnement correct comporte des défis crypto-économiques qui ne sont pas triviaux.
L’un des principaux défis est que, si nous voulons une fragmentation fondée sur la localisation géographique afin que les partitions géographiques de réseau n’empêchent que peu la cohésion intra-fragment (avec l’effet secondaire d’avoir des latences intra-fragment très faibles et donc des temps de blocs très rapides), alors les validateurs doivent disposer du moyen de choisir les fragments auxquels ils participent. C’est dangereux car cela permet des classes d’attaques bien plus importantes dans le modèle de la majorité honnête/non coordonnée, et donc des attaques très peu coûteuses dans le modèle de Zamfir. La fragmentation pour la sécurité de la partition géographique et lafragmentation par échantillonnage aléatoire pour l’efficience sont deux choses radicalement différentes.
Ensuite, il faudrait une réflexion plus approfondie sur la manière dont les applications seraient organisées. Dans un modèle de blockchain fragmentée ressemblant à ce qui précède, chaque « appli » serait sur un fragment donné (du moins pour les applis à petite échelle) ; cependant, si nous voulons que les applis elles-mêmes soient résistantes aux partitions, cela signifie d’une certaine manière que toutes les applis devraient être inter-fragments.
Une piste possible de résolution de ce problème consiste à créer une plateforme offrant les deux types de fragments. Certains seraient des fragments « globaux » offrant une haute sécurité, qui seraient échantillonnés aléatoirement, et d’autres seraient des fragments « locaux » offrant une moindre sécurité et disposant de propriétés comme des temps de bloc ultra-rapides et des frais de transaction moins élevés. Des fragments dont la sécurité serait extrêmement basse pourraient même être utilisés pour la publication de données et le passage de messages.
Quels sont les défis spécifiques au passage à l’échelle au-delà de n = O(c^2) ?
Il faut prendre en compte plusieurs considérations. D’abord, l’algorithme devrait être converti d’un algorithme à deux couches à un algorithe empilable à n couches ; c’est possible mais complexe. Ensuite, n / c (le rapport entre la charge de calcul totale du réseau et la capacité d’un nœud) est une valeur qui se trouve proche de deux constantes : d’abord, quand on mesure en blocs, un laps de temps de plusieurs heures, ce qui est un « temps de confirmation de sécurité maximum » acceptable, et ensuite, le rapport entre les récompenses et les dépôts (un premier calcul suggère un dépôt de 32 ETH et une récompense de bloc de 0,05 ETH pour Casper. Cette dernière a pour conséquence que si les récompenses et les pénalités sur un fragment sont escaladées à l’échelle des dépôts des validateurs, le coût de continuation de l’attaque sur un fragment sera de taille O(n).
Au-dessus de c^2, cela impliquerait probablement un affaiblissement des types de garanties de sécurité qu’un système peut fournir, et cela permettrait aussi à des attaquants d’attaquer des fragments de certaines façons sur de longues périodes pour un coût modéré, bien qu’il serait toujours possible d’empêcher un état invalide d’être finalisé et d’empêcher un état finalisé d’être annulé à moins que les attaquants ne veuillent payer un coût de O(n). Cependant, les récompenses sont grandes. Une blockchain fragmentée super-quadratiquement pourrait être utilisée comme un outil générique pour presque toutes les applications décentralisées et pourrait soutenir des frais de transactions qui rendraient son emploi presque gratuit.
Notes de bas de page :
- Arbre Merklix == Arbre de Merkle Patricia
- Les propositions ultérieures du groupe de NUS arrivent effectivement à fragmenter l’état, grâce aux techniques de reçus et de compactage de l’état que je décrirai plus loin dans ce document.
- On a ici quelques raisons d’être conservateur. En particulier, notons que si un attaquant lance des transactions nocives dont le rapport entre le temps de traitemen et les dépenses en espace de bloc (octets, gaz, etc.) est beaucoup plus haut que d’habitude, alors le système sera victime de très mauvaises performances et un facteur de sécurité s’avère nécessaire pour prendre en compte cette possibilité. Dans les blockchains traditionnelles, le fait que le traitement des blocs ne prenne que ~1-5% du temps de bloc a pour principal rôle de protéger contre le risque de centralisation mais sert aussi à protéger contre le risque de déni de service. Dans le cas spécifique de Bitcoin, sa pire vulnérabilité actuelle connue d’exécution quadratique limite sans aucun doute tout passage à l’échelle à ~5-10% actuellement, et dans le cas d’Ethereum, bien que toutes les vulnérabilités connues sont ou ont été éliminées après les attaques par déni de service, il reste encore un risque d’anomalies potentielles, en particulier sur une plus petite échelle. Dans Bitcoin NG, le besoin de celui-là n’existe plus mais le besoin de celui-ci reste présent.
- Une autre raison d’être prudent est qu’une plus grande taille d’état correspond à un débit réduit, puisque il sera de plus en plus difficile pour les nœuds deconserver les données d’état en RAM. Ils auront de plus en plus besoin d’accès aux disques et les bases de données, qui ont souvent un temps d’accès de O(log(n)), seront de plus en plus lentes en accès. C’est une leçon importante apprise de la dernière attaque par déni de service sur Ethereum, qui a gonflé l’état de ~10 Go en créant des comptes vides et a donc indirectement ralenti le traitement en forçant les accès à l’état à utiliser le disque au lieu de la RAM.
- Dans les blockchains fragmentées, il n’y a pas nécessairement de consensus synchrone sur un état global unique, et le protocole ne demande donc jamais au nœuds d’essayer de calculer une racine d’état globale ; en fait, dans les protocoles présentés plus loin, chaque fragment possède son propre état et pour chaque fragment il existe un mécanisme d’engagement (commit) sur la racine d’état de ce fragment, qui représente l’état du fragment.
- Si une blockchain classique devient susceptible de passer à l’échelle, la recommandation de l’auteur quant au chemin de migration est que la chaîne de l’ancien état doit simplement devenir un fragment de la nouvelle chaîne.
- Pour que ce soit sûr, quelques autres conditions doivent être satisfaites ; en particulier, la preuve de travail ne peut être externalisable afin d’empêcher l’attaquant de déterminer quelles autres identités de mineurs sont disponibles pour un fragment donné afin de miner au-dessus de celles-ci.
- Les récentes attaques par déni de service sur Ethereum ont prouvé que l’accès au disque dur est un goulet d’étranglement crucial pour le passage à l’échelle d’une blockchain.
- Vous pouvez demander : eh bien pourquoi les validateurs ne récupèrent-ils pas les preuves de Merkle au fil de l’eau ? Réponse : Parce que c’est une étape de ~100-1000 ms, et l’exécution de l’intégralité d’une transaction complexe pendant ce laps de temps peut être prohibitive.
- Une solution hybride qui combine l’efficience habituelle des petits échantillons avec la robustesse accrue d’échantillons plus grands est un système d’échantillonnage multicouches : avec un consensus entre 50 nœuds qui demande un agrément de 80% pour poursuivre, et si et seulement si ce consensus échoue à être atteint, revenir à un échantillon de 250 nœuds. N = 50 avec un seuil de 80% n’a qu’un taux d’échec de 8,92 * 10-9 même contre des attaquants avec p = 0,4, donc la sécurité n’est pas mise à mal dans un modèle de majorité honnête ou non coordonnée.
- Les probabilités données sont pour un fragment unique ; cependant, la graine d’aléa affecte O(c) fragments et l’attaquant pourrait potentiellement prendre le contrôle de l’un quelconque d’entre eux. Si nous voulons examiner simultanément O(c) fragments, deux cas se présentent. D’abord, si le processus de grinding est informatiquement limité, alors ce fait ne change rien au calcul puisque, même s’il y a maintenant O(c) chances de succès par round, la vérification de la réussite prend O(c) fois plus de travail. Ensuite, si le processus de grinding est économiquement limité, alors cela demande effectivement des facteurs de sûreté nettement plus importants (l’augmentation de N par 10 ou 20 devrait suffire) bien qu’il soit important de noter que le but d’un attaquant dans une attaque par manipulation motivée par le profit est d’augmenter sa participation à tous les fragments dans tous les cas et donc c’est le problème que nous étudions déjà.
Document d’origine : Vitalik Buterin – Sharding FAQ
Traduction : Jean Zundel – Qu’est-ce que la fragmentation ou sharding ?